ARC115F Migration

题意 ： 给出一棵 个节点的树，点有点权 。

树上有 块石子，记第 块石子的位置为 ，则当前局面的“不稳定度”定义为 。

给出石子的初始位置，你的目标是将第 个石子移动到节点 ，每次只能将一个石子移到相邻的节点（允许多个石子放在一个节点上），最小化过程中不稳定度的最大值。

，时限 。

---

考虑二分。

记 为初始局面， 为终止局面。

记 为局面 的不稳定度（若不稳定度相同则比较字典序）， 为局面 所能到达（有 约束）的最小的 。

不难发现，由于操作的可逆性， 能到达 当且仅当两者能到达的不稳定度最小的局面相同。

问题转化为求 。

---

根据操作的可逆性，若 能互相到达，则 。

那么，我们每次找出一个可达的 使得 ，重复若干次即可得到最小的 。

为了便于维护，我们每次只考虑一个石子的连续移动，将这个石子（合法地）移动到一个 更小的位置。

可以证明，若不存在这种方案，则不存在任意 使得 。于是只用考虑这种移动就好。

显然这样的移动最多 次。

我们需要快速求解 ： 从 点移动，所到的点权不超过 ，能到达的最小点权。特殊地，若点权不能变小，则置为 。这个随便 dfs 预处理。

然后再用堆维护每个石子的最小出边即可。

---

可以发现其实不用二分，只需每次挑一步最大不稳定度最小的转移。

记 为路径 的最大权值。

这样，我们对每个 记 表示 点满足 且 最小（若相同，则比较 的权值）。

当我们移动 点时，必然会前往 。

这样的复杂度为 ，已经足以通过。

---

的求法：考虑按 从小到大加入点的过程，建立类 Kruskal 重构树。然后再次从小到大考虑 目标就是找到 与更小的点的 ，容易倍增求算。复杂度为 。

建立一张新图，对于 ，连有向边 ，边权为 （即不稳定度的增量）。这形成一棵内向树。

贪心时，每次走 最小的边。

• 性质 ：若 ，则有 。也就是说，在新树上越浅边权越大。

  证明 ： 的分布如下图：（其他一些情况可以视为该图的退化）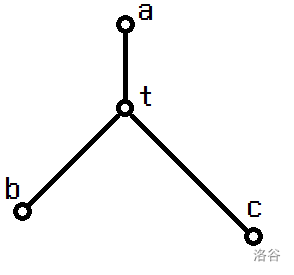

  

  记 。

  若 最大或 最大：此时 ， 选择 ，矛盾。

  因此只可能是 最大，则 .

  结合 则有 。

于是，我们可以直接给边按 从小到大排个序（也是从浅往深，若权值相同则比较深度），然后依次移动就是。

这里我们可能同时移动多个石子，用 xor Hash 维护集合特征，并记一个集合大小以计算不稳定度的变化。

可以把二分加回来以简化实现。

复杂度 。