Luogu5525 [Ynoi2012] WC2016 充满了失望

题意：给出平面上的一个点集 和若干个圆。对于每个圆，判定其是否完全在 的凸包的内部。

保证圆的半径变化不超过 时答案不发生变化。，时限 。

---

将凸包拆分成上凸壳和下凸壳。我们只需分别判断圆是否在 上/下 凸壳内部。

下面只介绍上凸壳，将 坐标翻转即可转化为下凸壳。

记 为点集 的上凸壳内部的区域。

记 表示能完全放入平面区域 中的半径为 的圆的圆心的集合。

考虑随着 的增大 会如何变化。

若将 描述为半平面交，则变化相当于每个半平面收缩了 单位距离。

---

将询问离线，按 从小到大处理，我们只需要维护半平面交的收缩，并判定圆心是否在其中。

在收缩的过程中，有些半平面可能不再在凸壳上，需要将其删除。

每个半平面只可能被两侧的半平面迫害掉，用堆维护每个半平面被迫害掉的时间。

如何计算 迫害 所需时间？

这是初中数学基础题：做两条角平分线，取交点到 的距离。

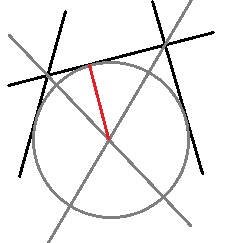
当某个半平面被删除时，重新计算两侧的半平面的迫害时间。

对于一个正确的收缩凸壳，容易二分判定圆心是否在其中。

用并查集维护序列，能支持删除某个元素，快速查找某个元素的前后继。

复杂度 。