AGC025E Walking on a Tree

题意 ： 给出一棵 个点的树以及 条树上简单路径。

要求给简单路径定向。定向后，树边 的边权定义为：

• 边权初始为 。
• 若存在某条路径以 的方式经过，边权加一。
• 若存在某条路径以 的方式经过，边权加一。
• 最终的边权可能为 。

最大化边权和。求出这个最大值，并给出定向方案。

，时限 。

• 加强版：。

---

感谢 @Kinandra 大神的指导。

对于第 条边，记其被路径经过的次数为 ，则这条边的权值上界为 。

猜想存在一种方案使得每条边的权值均达到上界。

---

每次考虑某个叶节点 与连接该叶节点的唯一的边 （编号为 ）。

• 若 ，直接将 与该边删除。

• 若 ，说明存在恰好一条路径的端点为 （这条路径一定经过边 一次，方向不关心）。将其端点更改为 ，然后将 与边 删除。

• 若 ，则要安排一条从里到外的路径和一条从外到里的路径。

  任选两条经过边 的路径 ，定向为 或者 。

  两种方案对应下图：

  

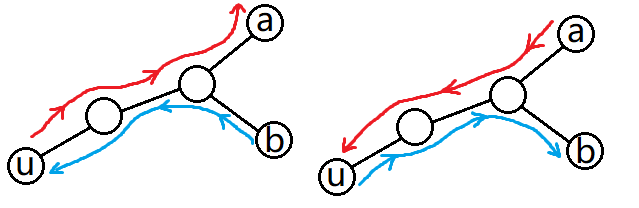
  记两条路径的的分叉点为 ，不难发现，路径 上的边都被正反经过各一次，完成指标。

  而 上的边要么方向是 ，要么是 ，不难发现，这等价于（可以自由选择方向的）路径 。

  于是，我们将 上的边设为“已完成”（这可以暴力，每条边只会被完成一次）。然后删去路径 ，并加入路径 。

  对于其他端点为 的路径，将端点 改成 。

  最后将 与边 删除。

  • 还要说明一下我们没有破坏 的前提条件。

    对于 上的边， 减少了 ，但他们的贡献已经达到上界，不用再考虑。

    对于 上的边， 没有变化。其他边的 也显然不变。

    于是，根据归纳法，该算法总能找到符合要求的解。

---

具体实现时，随意指定一个节点作为根进行 dfs，按后序遍历删除节点，这样每次删除的都是叶子。

处理节点 的返祖边时，需要尝试找出两条一段在 子树内一段不在的路径，可以使用 std::set 维护。

若找不到只能找到一条，则不操作路径。

若找到两条，则将它们打上删除标记。并新加入一条路径，表示不重合部分的决策。

（注意这条新路径的决策会影响两条旧路径的决策，在最终回答问题时需要推算决策）

然后将重合部分的链打上标记，标记了的边自动获得 的满贡献。这可以用树状数组链加实现。

复杂度为 。