ARC089D ColoringBalls

发表于 更新于 分类于 ， ， 阅读次数：

题意：有 个白色的小球排成一排，有一个长为 的字符串 。

接下来进行 次操作。

对于第 个操作，选择一段连续的小球（可以为空），若 则将这些球染成红色；若是 ，则将它们染成蓝色。

由于染料的特性，不能直接用蓝色来染白色。

求在进行完所有操作后，所有小球的颜色序列可以有多少种。答案对 取模。

，时限 。

首先考虑如何判定某种颜色序列是否能被生成。

  • 连续的一段有色区间

    可能分布为 红蓝红蓝...红蓝红。

    考虑有怎样的构造方案，如下图：

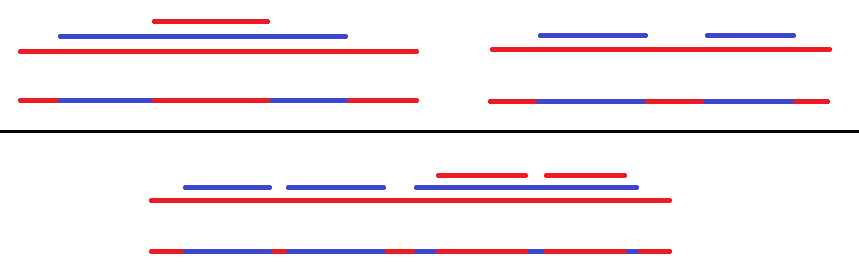
    • 先考虑染色次数：

      若有 个蓝色段，则所需的染色次数为 次，红色和蓝色的次数不定，在 之间。（特殊地，若没有蓝色，则只需染一次红色）

    • 再考虑染色顺序：

      若我们决定染 次蓝色，最好的方案是：先染一次红色，再染 段蓝色，然后染一大段蓝色，再在这段蓝色上染完剩下的红色。

    • 总结操作序列的要求：满足个数要求。且最前面是 ，第二个是 。没了！

  • 多段有色区间

    设有 个纯红色段，以及 个杂色段。

    则在操作序列中取出 个尽量靠前的子序列 ，再取出 个尽量靠前的 。后者用于处理纯红色段。

    然后，从左到右考虑，将第 个 分给第 大的杂色段，并在后面取走想要的若干个操作。

    若发现无球可取，则无解。

    形式化地，记第 个 后面剩余的操作数目为 。

    第 个杂色段的内部段数和为 。（降序）

    则对于所有 ，都要满足 。

接下来考虑计数。

枚举 ，然后我们得到了 。

先考虑在得到 的情况下，如何计算颜色序列的方案数。

将每一个“颜色段”看做一个盒子。

我们发现，对于一个 ，会产生 个至少有一个球的颜色段，以及 可以为空的颜色段（两端的红球）。

对于 ，会产生 个至少有一个球的颜色段。

对于白色的部分，会产生 个至少有一个球的颜色段，以及 个可以为空的颜色段（两端的白球）。

综上，非空盒的个数为 个，而可空盒为 个。

总球数为 ，容易用组合数求出方案。

此外，杂色段和纯红色段之间的顺序也需要考虑。

首先是杂色段和纯红色段混合的方案数，显然为 。

然后是杂色段内部顺序数，即 序列的不同排列数，这个使用 求解。

设 表示填写了 ，目前 ，且 的方案数（不同排列数）。

枚举在 中选多少个 ，则有转移 ：

式子中 是将 个 归并到目前的 中的方案数。

要求 且 。

最终的答案是 ，根据第二维的 计算贡献系数。

使用前缀和优化，即可做到 。

算上枚举 的复杂度，总复杂度为 。由于常数非常小，可以轻松通过。