CFgym102759B Cactus Competition

XXI Open Cup, Grand Prix of Korea

题意：给出两个序列 。

构造一个 的矩阵 ，其中 。

从 出发前往 ，其中只能经过权值非负的位置（包括起点和终点），且只能向右或向下行走。

求有多少组 是可达的。

，时限 。

---

先考虑如何判定 是否可达。

初看本题，没有什么好的切入点，尝试发掘一些简单的性质。

• 若 ，则说明有一行（ 的那一行）全为负。

• 若 ，则说明有一列（ 的那一列）全为负。

若满足上述两个条件之一，则说明 不可达。下面讨论它们不满足的情况。

• ，则说明有一列（ 的那一列）全非负。

• ，则说明有一行（ 的那一行）全非负。

我们发现了一个有趣的性质，在本题中，“存在一行全为负”否定后可以导出“存在一列全非负”。

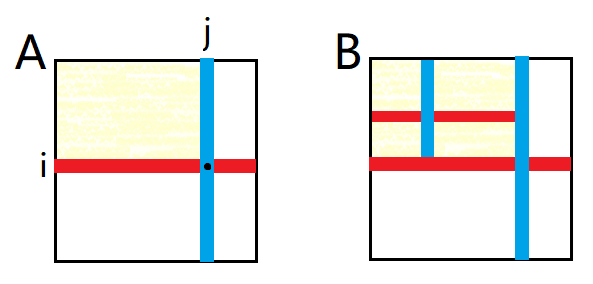
画出这非负的一行一列，记为 ，如图 。

考虑构造一种方案，从左上角先来到 ，再前往 。

若左上方黄色区域内存在一行与一列均为负，显然无解。否则，黄色区域内必然存在一行或一列非负。如图 。

这样，就将左上角区域缩小了，不断重复，即可到达起点。类似地，也可以到达终点。

根据上面的观察，只需要排除下列四种阻断情况即可：

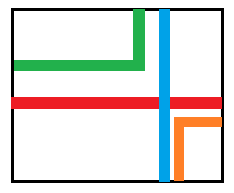
四种阻断均不存在 可以从 到达 。

---

接下来考虑如何计算答案。

对于全负的行，会将问题分成若干段子问题（也可以看做提供下界）。下面我们不再关心这类限制。

枚举 ，考虑有多少 满足 ：

• 找出第一个 使得 。则 的都满足条件。

综上，蓝色和红色隔断为每个起点 限制了一个终点的区间。

对于图中绿色和橙色的阻断，相当于直接除掉了一些起点和终点。

• 绿色，左上角阻断（橙色右下角阻断类似）

  对于起点 ，若存在 满足 且 ，则将 删除。

  枚举 ，考虑所有 的贡献。

  找到最小的 使得 （ 从大到小排序后前缀编号 ），则前缀 都是负的。

  为了尽量向上延伸，只需找到 中最小的一个，记为 。

  然后找出一个最大的 满足 （单调栈 + 二分），则区间 之间的起点都被删除。

先去除不合法的起点终点（可以用差分），然后若干次区间求和即可。

复杂度 。