Luogu7601 [THUPC2021] 区间本质不同逆序对

发表于 更新于 分类于 ， ， 阅读次数：

题意：给定一个长为 的序列 。

有 次询问，每次询问给定一个区间 ，求 。

，，时限 ，空限 。

考虑莫队。

先考虑左端点移动的贡献。右端点在将序列和值域同时翻转后可以转化为左端点。

记 是 下一次出现的位置。

当 减小至 ：

考虑新增的本质不同逆序对。

当 移动到 时， 中 的 会构成逆序对 。（当然，不保证全是新的）

而对于所有 的 ， 都必然与 重复。

对于所有 的 ，若 在 中出现过，则重复，否则不会重复。

也就是说，我们要计算的是 ： 在 中出现过，但在 中没出现过，且 的数的种类数。

记 内 的数的种类数。不难发现上面要计算的东西

我们每次需要计算的一组 的 是相同的。

问题转化为了 个 的计算。

将 看做三维平面上的点 ，则有：

可以先预处理 ，这样上式变为 ：

这是三维偏序。

先将 按照 排序，逐次加入，消去了 的约束。

然后我们需要一个维护动态二维偏序的数据结构。

将 的二维平面分成 个 的块（称作大块）。对这些块维护二维前缀和。（红色）

将每个“大块”（按两个方向）分成 个 的块（称作“中块”）。对每一行 / 列“大块”维护内部 个“中块”的二维前缀和。（蓝色）

又将每个 “大块” 分成 个 的块（称作“小块”）。对每个“大块”维护内部“小块”的二维前缀和。（绿色）

然后我们剩下的就是 ： 询问两条边界附近宽度不超过 的区域。（黄色）

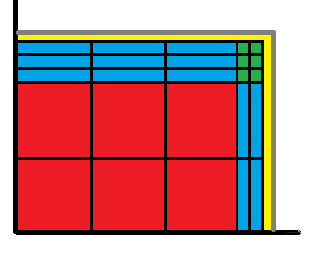
对于黄色部分，我们不再维护前缀和，转而考虑每个点的贡献。

点在某个询问的黄色部分的充要条件：该询问覆盖了该点，但没有完全覆盖该点所在的小块。

注意到询问的端点形如 ，只有 个本质不同的端点，且符合上述条件的端点只有 个（需要对 进行重标号，避免重复），于是可以暴力枚举并进行贡献。

时间复杂度 ，空间复杂度 。