ARC068D Solitaire

题意：将 按顺序全部加入双端队列（可加头可加尾），再取出（可删头可删尾）。

将取出的牌按顺序排成一个序列，称之为「删除序列」。

求有多少种删除序列，使得 排在第 个。答案对 取模。

，时限 。

---

感谢 @BILL666 题解的指导，学到许多。

先来考虑如何判定一个序列是否是「删除序列」，且满足 排在第 个。

观察产生删除序列的过程。

首先，双端队列填满时，一定形如单谷。从谷底 向左右看，都是上升序列。从外往里看则是下降序列。

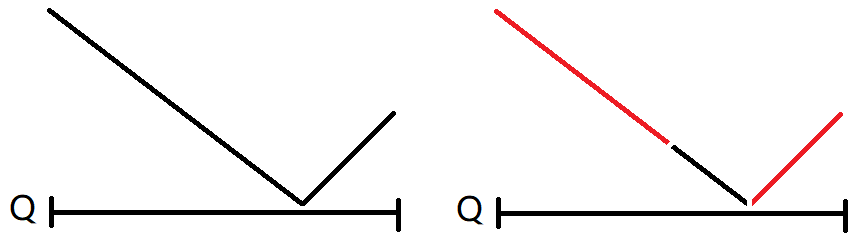
取出时，在取到 之前，相当于将两个下降序列归并。于是，前 个数需要满足：能够划分为两个下降子序列。称这个性质是「双股的」。

在取出 之后，我们便不再关心后面数的状况，但仍然要考虑其方案数。

此时，队列中的 个数一定是有序的（谷底的一侧被拿完了）。

除了最后一个数以外，每一步从队列的两侧取都会得到不同的结果，于是方案数为 。

不妨强制每次都取较大的，不难发现，这样（仍然在做归并）构造出的一定是双股序列，且这是唯一一种得到双股序列的办法。

于是，我们统计第 个位置为 的双股序列个数，再将答案乘以 即可。

根据 定理，「能划分成两个下降子序列」 「 不存在长为 的上升子序列（三连升）」。

可以进一步发现，一个排列与其逆排列的 「双股性」 总是相同的（这不会改变偏序关系）。故「第 个位置为 的双股序列个数」等于「第 个位置为 的双股序列个数」。

---

考虑 。记 表示 元排列中第 个位置为 的双股序列个数。

边界：。

转移：

若 ，则其不可能是某个「三连升」的一部分，于是可以直接删除。

若 ， 是某个下降序列的开头。另一个下降序列的开头则是 。

考虑排列的第二项 ，若 ，则可以将其直接删去。故 。

若 ，则构成三连升，不合法。

若 ，合法，故

综上：

进一步推导可得：

直接 ，复杂度为 ，可以通过。

---

在 Luogu4769 [NOI2018] 冒泡排序 中我们得到，双股序列的个数可以写成简单的组合数。所以我们也有希望在本题中更进一步。

将式子写成主动贡献，尝试编一个组合意义：路径。

• 当位于 时，可以前往 或 。但不能越过直线 。

先不考虑「不能越过直线 」的限制，从 到达 的方案数显然为 。

「越过直线 」等价于「达到直线 」。我们将不合法方案第一次触碰 之后的路径根据 翻转。

于是，不合法方案与「从 到 的路径」一一对应。

综上我们能得到：

复杂度 。