AGC004F Namori

发表于 更新于 分类于 ， ， 阅读次数：

题意 ： 给出一张 个点 条边的连通图，满足 。

初始时每个点都是白色，每次操作可以选择一条边，若两个端点的颜色相同，则可以将两个端点的颜色取反。

目标是将所有点变为黑色，求出所需的最小步数，或指出无解。

，时限 。

  • 为奇数时无解

    每个点最终一定参与了奇数次操作， 个奇数求和，得到奇数次对点的影响。

    一次操作影响 个点，对点的影响只可能是偶数次，矛盾。

  • 为偶数，且图是一棵树

    注意到树是二分图，将树黑白染色，操作能进行的条件就变为“端点异色”，且作用等价于将黑点移动一步。

    目标是将黑白位置对调。

    操作只能移动，不能改变黑白点的个数。由此可以发现，若黑白染色后，两种颜色的点不相同，则必然无解，否则有解。

    考虑某个子树连向父亲的边，若子树内有 个黑点，以及 个白点，那么该边至少要用于向内或向外运输 个黑点。可以归纳证明这同时也是可以取到的。

    具体地，将黑点的点权置为 ，白点的点权置为 ，记 的子树点权和为 ，则答案为 。

  • 为偶数，且图是一棵基环树，环长为偶数

    此时图仍然是二分图，前面的转化仍然成立。

    在环上断掉一条边，看做树的情况，然后单独考虑该边的使用次数。

    若按照指定方向使用了 次，则对 的影响如下 ：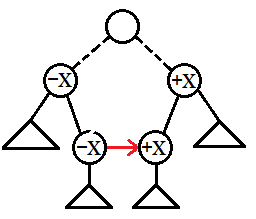

    将会受到影响的点的贡献写成 的形式，即转化为经典问题。

  • 为偶数，且图是一棵基环树，环长为奇数

    此时图不再是二分图了。

    先断掉一条环上的边，然后黑白染色。

    这条特殊的边使用规则和其他边不同，每次可以把黑黑变为白白，或者白白变为黑黑。

    查看整棵树的权值和 ，若为偶数，则可以利用这条边消除之，否则无解。

    而这条边的使用次数也可以恰好为 ，证明略去。

    考虑完这条边的影响后，完全转化为树的情况。

复杂度 。