AGC006E Rotate 3x3

题意：有一个 的矩阵，初始时，位置 上的数字为 ，下图是 时的情况：

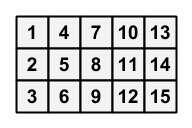
每次操作可以将一个 的子矩阵旋转 ，如下图 ：

给出矩阵的目标状态，判定是否能通过若干次上述操作达到。

，时限 。

---

• 性质：每一列的三个数是不会分开的，但可能上下翻转。

于是，将三个数映射成一个数，且有正负之分，问题转化为 ：

给出长为 的数组 ，与目标状态 ，每次操作可以指定 并交换 ，并将 均乘以 。

若 中的元素不可能从 中得来，则无解。

• 性质：操作不能改变某个数所在位置的奇偶性。

若一个数的起点和终点位置奇偶性不同，则无解。

• 性质：操作是可逆的，且逆操作为操作本身。

可以把问题转化为由 操作到 。

先不考虑正负，问题相当于利用交换 将数组排序。

按照奇偶分为两个序列，分别冒泡排序即可。

计算出排好序后的正负，再尝试将全部负数修正为正数。

先考虑排好序后如何调整。

• 若奇位置或者偶位置的负数为奇数个，则必定无解。

  因为奇位置和偶位置是已经有序的，要想结束时仍然有序，一定只能进行偶数次交换，故不可能影响奇数次正负性。

先消去所有在奇数位置的负数。

将负数两两配对，假设为 。先将 运到某个位置 ，操作 将其变号。再将 运到 ，操作 将其变号。最后将两者运送回去。

运送 产生的交换都和自己抵消，不会影响正负性和顺序，于是我们就这样消去了一对负数。

而对 的两次操作虽然会牵扯到偶数位置，但也抵消了。

故有解的充要条件是，奇位置或者偶位置的负数为偶数个。

对奇位置的交换操作会影响两个奇位置和一个偶位置，对奇位置的负数个数奇偶性无影响，而对偶位置的负数个数奇偶性有影响。

于是，计算出两者的逆序对数目（即为交换次数）即可，复杂度为 。