AGC007D Shik and Game

题意： 初始时 Shik 君在数轴的原点，出口坐标为 。数轴上有 只小熊，第 只小熊在 位置。

Shik 君拿着 块糖果出发，每走一个单位长度要花费一秒。

到一个小熊的位置时，他可以送给这个小熊一块糖果，这个过程不花时间。

小熊收到糖果后， 秒以后会在它所在的位置产生一个金币。拾起所在位置的金币也不需要时间。

Shik 君想知道，他从出发到收集了所有金币抵达出口，最少要花费多长时间。

，，时限 。

---

将 从小到大排序。

考虑简化决策，注意到数轴上某个位置只能被经过奇数次。

若每个位置都只能被经过一次，那么策略将是单调的 ： 一直向右，在每个小熊处都等待直到拾得金币。这显然并非最优策略。

所以，我们应当允许适当的回头，在等待这只小熊的同时，先给后面的熊发糖，然后及时回来。

因此，同一个位置被经过三次是需要被允许的。但是若经过五次，可以调整为三次，且不会变劣，如下图：

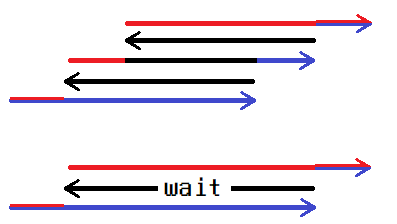
其中红色表示最晚到达某一位置的方案，蓝色表示最早到达某一位置的方案。显然，红色越晚越好，蓝色越早越好。

下图中的红色均不早于上图中的红色，蓝色均不晚于上图中的蓝色，故不会更劣。

于是，我们有关键结论：某个位置只有可能被经过一次或三次。

---

由此，可以考虑 。

设 表示 的金币都已经拾起，且目前在 位置的最小耗时。

转移时，枚举经过三次的一段小熊，则有 ：

其中 是从 出发，三次经过将 中的熊都搞定所需时间。

有 。

其中 ， 指往返的代价， 指等待最后一只熊的代价。

无论如何转移， 的和都是 ，可以忽略，

于是有

此时大力分类转移。

• 转移为 ，取 的最小值即可。

• 转移为 ，取 的最小值即可。

其中，第一类转移的 是一个前缀，且两种转移的分界线随着 的增加单调右移。

使用单调队列维护即可，复杂度 。