CF1239F Swiper, no swiping!

题意： 给出一张无向连通图，删除一个既不是空集又不是全集的点集，使得剩下的点度在 下不变。或指出无解。

多组数据，，时限 。

---

没有经典的模型转化，让人一时没什么头绪。先随意得到些性质，不断考虑特殊情况。

称点度 的点为“ 度点”。运用启发式思维，快速找出几类可能的构造。

• Case #A

  若存在 度点，则只保留该点即可。

  接下来只需考虑只有 度点的情况。

• Case #B

  若存在 度点之间有边，则保留这两个点。

  进一步地，若存在两头是 中间是 的路径，且路径内部没有其他边，则保留该路径。

  不难发现，由于图联通，若存在两个 度点，则必然存在这样的路径。

  这可以从任意一个 度点 bfs 得到。不难证明两个 度点之间的最短路必定满足要求。

• Case #C

  若存在 度点形成的环，且内部没有其他边，则保留这个环即可。

  不难证明 dfs 中树边产生的环中最小的环一定满足要求。

• Case #D

  我们还需讨论的图含有至多一个 度点，将其去除之后，则是一棵 度点森林。

  而且，不难证明 度点是必然存在的 ： 由于 度点形成森林，则叶节点必须与 度点联通（否则不可能是 度点） 。

  因此，森林中所有的叶子都接到了 度点上。（非叶节点也可能接到 度点上）

  又不难发现，由于一棵树至少有两个叶子，故 度点实际的度数 ，那么就 。

  于是考虑构造如下图的方案：

  

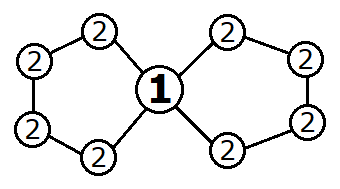
  若有森林中有 棵树，只需在某两颗棵树各选取一条叶子之间的路径。

  实际上，森林中不可能只有一棵树，证明如下：

  考虑只有一棵树的情况，设节点数为 ，则节点度数和 。

  而内部度数和 ，故连向 度点的度数和 ，矛盾。

注意，最终还需要判定得到的方案是否为整个图，此时无解。

代码实现较为繁琐。