Luogu4331 [BalticOI 2004]Sequence 数字序列

题意 : 给定序列 ，构造递增序列 ，使得序列 和 的各项之差的绝对值之和即 最小。

，时限 。

---

考虑 。

首先将 同时减去 ，这样约束可以转化为 。

设 表示考虑了前 个数，且 ， 的最小值。

有转移

记 ，则 。

于是，问题变为 ： 维护序列 ，支持下列两种操作 ：

将 分为若干段线段维护。只需维护拐点。

当插入某个绝对值函数 时， 前面的线段斜率均 ，后面的线段斜率 。此时可能需要插入两个 。

最后两条斜率为 的线段可能合并。

我们用拐点 表示 ，拐点重复 次则 。用堆维护拐点即可。

我们维护的折线如下图：

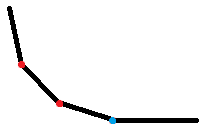
最终的最优解是 的最后一个拐点(蓝色)处。

我们已知 (处在斜率为 的部分)，要求出 。

为 轮的最后一个拐点 。

复杂度 。