Luogu4437 [HNOI/AHOI2018]排列

题意：给定两个长为 的序列 。其中

对于一个 的排列 ，若对于任意的 都有 ，则称为好的。

定义该子序列的权值为 。

求权值最大的好排列，或指出好排列不存在。

，时限 。

---

在原序列中，若 ，则连边 之间。说明 一定要排在 前面。

若最终的图有环，则无解。

每个点本应恰好有一条入边，构成基环外向树，但连向 是个例外（可以忽略这条边）。

因此，若无环，则必然是森林。

原来的限制形为：只有选择了所有祖先，才能选择子孙。

也即，找出一种深度递增的遍历序使得权值和最大。

一种显然的贪心原则是：将较小的权值放在前面，将较大的权值放在后面。

可以发现，对于 最小的节点 ，若已经可以取，则必然取。

于是，我们可以将 与 捆绑，表示两者的决策一致。

---

将捆绑后的节点缩成一个点，如下图所示

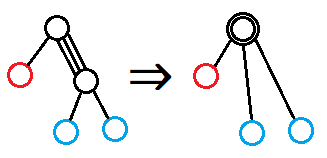
考虑缩出来的“大点”（内里是一个序列），这将问题变得广义了，原先的单点比较顺序变为了“序列”比较顺序。

考虑序列 ，考察 在前更优的充要条件。（不难感知，这是个全序关系）

记 ， 类似。

所以，两者的优劣就在于比较 与 ，即 与 ，恰是平均值。

于是乎，用堆（可用 std::set 实现）维护目前所有点，重复下列操作 ：

• 找出目前权值最小的点 。

• 若 没有父亲，则将 接入答案序列的后端。

• 若 有父亲，则将 与父亲合并，并更新堆。

复杂度 。