Luogu5896 [IOI2016] aliens

题意 ： 有一个 的矩阵，以及 个关键位置。

现在可以操作 次，每次覆盖如下条件的一个矩阵 ：

• 是正方形

• 主对角线是原矩阵主对角线的子集

需要保证每个关键位置至少被覆盖一次，且最小化至少被覆盖一次的格子数目。

，，时限。

---

首先不难发现，某个关键位置根据主对角线翻转后是等效的。于是我们将所有 整理为 的形式。

接下来又能发现，若对于 ，若 ，则所有能覆盖到 的方案都能覆盖到 。

于是，我们保留了关键点的“上包络线”，如图 ：

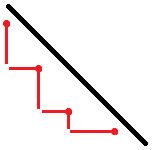
由此又能简化决策 ： 若一组覆盖矩形中，有某个矩形的边界不穿过（卡在）任何一个关键点，则可以往回缩得到更优秀的解。

接下来开始 求解。设 表示使用了 个矩阵，最后一个矩阵主对角线结尾在 ，且覆盖了 前 行所有关键位置的最优解。

枚举连续一段行 ，并将其中所有关键点一并覆盖。

则有转移：

其中 表示用一个矩形覆盖行 中所有关键点的花费。

根据上包络线的性质，当 时 处的矩形不会覆盖到 前未覆盖的部分。

于是新覆盖的位置可以这样计算 ：

记 为第 行关键点的位置，若没有，则为 。

先算出 ，表示需要覆盖的最靠左的关键位置。

于是，需要新加入的矩阵的边长即为 。

新覆盖的面积即为

同时注意到由上包络线的性质，，故用 代替之。

于是记 ，则有

显然可以以 为变量进行斜率优化，复杂度为 。

本着 “ 做不了就是凸的” 这一经典论断，我们大胆猜想本问题具有凸性。可以打表验证。

然后就是个 二分了……

复杂度 。