Luogu6383 『MdOI R2』Resurrection

发表于 2025-02-25 更新于 2025-02-26 分类于算法竞赛，题，洛谷阅读次数：

题意：给出一棵个点的树，边编号为。

保证对于任意一个节点，从到号点的简单路径都不经过任何编号小于的点。

按照如下步骤生成一张包含个节点的无向图：

选取一个的排列，然后依次进行次操作。

在进行第次操作时，首先删除树中编号为的边，然后，记和分别为当前树中与联通的所有点中，编号最大的点，并在图的号点和号点之间连一条边。

求对于给定的树，按上述方式一共可以生成多少种本质不同的图。图和本质不同当且仅当存在和满足在中不存在边，而中存在。

答案对取模，，时限。

题目中的性质是说，若以点为根，则所有向下的路径都是单降的。

考虑简化图的构造过程。我们发现，对于树上的一个联通块，最大权值一定在最浅点取得，于是可以改为“将两个联通块的最浅点连边”。

只有这里用到了关于编号的性质，所以我们可以把编号的性质忘掉，保留这一条规则作为代替，也是等价的。

从该规则出发，不难归纳证明：最终产生的是一棵树。

实际上，可以看做按照排列进行“边分治” 的产物，由于每次连接两个连通块的最浅点，故连边方法唯一，因此问题对应到本质不同边分治方案数计数。

但实际上这个模型比原来的生成方式更复杂了，故不从此处出发考虑。

现在问题仍然较为复杂，随机作出前提假设，发掘一些性质：

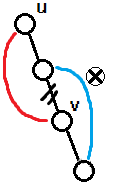
而对于一组不交叉（只有包含或相离）的连边方案，总能够造出对应的边分治顺序。

每次选取浅侧最浅且没有被其他边包含的边断掉，这样就能转化为子问题，归纳即可证明。

于是，问题转化为：每个点都会向祖先连边，且连边不交叉，求方案数。

考虑树形，这里我们有两种方向，第一种是考虑子树向自己连的边，一种是考虑祖先向自己连的边。

子树集合是一棵树，在处理“路径不交”时较为复杂。而祖先集合是一条路径，更为简单。

于是考虑设表示的祖先有个点可以向下连边，子树中的连边方案数。

边界：当是叶子时，

答案：

转移：

枚举与祖先中从高到低的第几个连边，若与第个连边，则连完后还能向下连的有祖先以及自己，共个。

不难用前缀和优化做到。