Luogu6799 「StOI-2」独立集
题意 :给出一棵
答案对
先考虑链上的子问题。
将所有区间按照终止点从小到大排序,设
对于每一个区间
也可以不选择任何路径,于是
上树之后,按照路径最浅点(LCA) 的深度从大到小排序处理。
设
在
若选择(满足
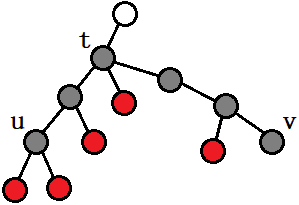
考虑维护
但是,可能构造出
不难发现,在灰色路径中,
(特判
对于点
不缺儿子的情况直接乘
这样,设
对于缺两个的情况,使用一棵额外的线段树维护区间积即可。
维护
可以转化为子树乘和单点查询,使用线段树即可做到
题意 :给出一棵
答案对
先考虑链上的子问题。
将所有区间按照终止点从小到大排序,设
对于每一个区间
也可以不选择任何路径,于是
上树之后,按照路径最浅点(LCA) 的深度从大到小排序处理。
设
在
若选择(满足

考虑维护
但是,可能构造出
不难发现,在灰色路径中,
(特判
对于点
不缺儿子的情况直接乘
这样,设
对于缺两个的情况,使用一棵额外的线段树维护区间积即可。
维护
可以转化为子树乘和单点查询,使用线段树即可做到