AGC006F Blackout

发表于 更新于 分类于 ， ， 阅读次数：

题意：有 的矩阵，初始时有 个格子是黑的。

若 都是黑色，则可以把 涂黑。

问最终有多少个黑色格子。

，时限 。

转化成一个更容易理解的题意 ：有一个 个点的有向图，若有连边 则可连边 。（即自动补全三元环）

问最终的边数。

显然需要对每个弱连通块分别处理。

手玩能发现，若是一条链，则会有三轮的规律。

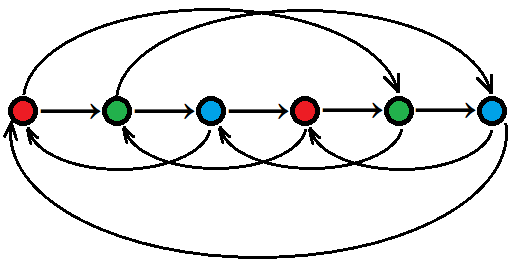
每个红点会向所有绿点连边，每个绿点会向所有蓝点连边，每个蓝点会向所有红点连边。

若是二分图，则不会有多余的边。

若是非三倍数的环，则会形成完全图。

总结一下规律：

对图进行三染色，若染色成功且需要三种颜色，则最终形成一个三分图，图中的每一部分都向下一部分连边。

  • 证明：若染色成功，则显然不能再得到三分图之外的边。

    我们停止加边只有可能是这样一种情况 ：对于所有异色三元组，要么已经形成三元环，要么只有不超过一条边。

    不难发现此时图必然不是弱连通的。

若三染色失败，必然形成完全图。

  • 证明：先忽略导致染色冲突的边，建立三分图。然后加入这些边，一条错误的边在三分图中必然导出一个二元环。

    二元环可以产生自环，而自环会进一步导出二元环。如此往复不难发现最终会得到完全图。

若需要的颜色不足三种，则不能加入任何边。这个比较显然。

综上，我们对每个弱连通块分别处理：

  • 若三染色失败，贡献为 。

  • 若三染色成功，且需要三种颜色，设三种颜色用量分别为 则贡献为 。

  • 若只需要不足三种颜色，则贡献为原来的边数。

复杂度 。