题意:给出一颗 个节点的树 ,以及关键点集合 。
定义树上邻域 。
令 ,求 。即本质不同的关键点邻域个数。
,时限 。
牛逼题。
特殊情况:
先统计所有
的贡献,最后加 。
这样,对于同一个 ,有 。
若 中有若干个 同构,考虑在 最小的 处将其统计。(关键思想)
先观察怎样的
会相同,如下图 :
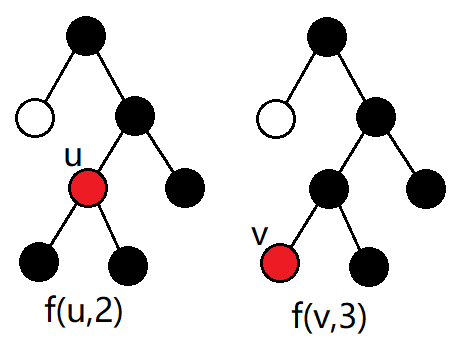
对于同一个关键点 ,只有若干个
是有贡献的。考虑某个 能贡献的条件。
首先我们要求 ,设 为 到最远点的距离,则有 。
此外,考虑同构。以
为根,考虑另一个关键点点 ,设
。
显然,除了 之外,其余的
。
若 ,则 两者都能覆盖除了 上方的所有部分。
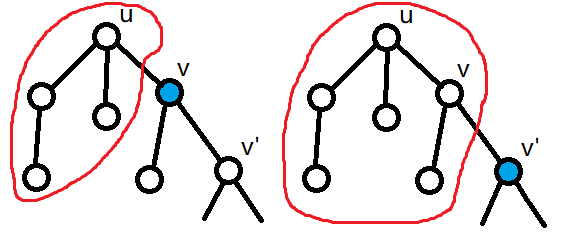
(如图,蓝色点为选择的
,红色部分为
需要覆盖的部分)
设 为以 为根时 子树外的点到 的最远距离。
则有 即 。排除掉这些 即可。
这也说明了,对于某个
,能贡献的 是一个前缀。
现在,要对每个关键点 求出
。
不难发现,这里的
可以只考虑相邻节点。则变为
而所有 可以使用 树形 求出。
一般情况
在 中,若 为关键点, 的下界必然是 ,但对于非关键点则是其他数。
考虑对于非关键点 ,使得 有贡献的最小的 。
以 为根,考虑某个关键点 。若能覆盖 所在的整个分支,就能“夺过” 的邻域。
不难发现,当
更大时,上述关系仍然可以成立。
于是,下界即为:覆盖某个含关键点的分支所需的最小 。
也可以使用
树形 求出。
知道了各个
的上下界,容易得到答案。
复杂度 。

