Loj#6039 「雅礼集训 2017 Day5」珠宝

题意：01 背包问题。

体积 ，背包总容量 ，时限 。

---

这是一类特殊的 卷积问题。

不难想到，先将同类物品合并，再将各个合并后的数组卷积。

同类物品中，一定选择价值较大的若干个。此时产生的数组是上凸壳。

暴力转移的复杂度是 ，不能接受。

转移大小为 的所有物品时，显然模 不同余的位置之间没有影响，我们对每个余数分别计算。

现在则变成了一个单调的数组和一个上凸的数组的 卷积。

设 单增， 单增且上凸，则 卷积相当于 ： 对各个 求 。

画出图来是这样的：

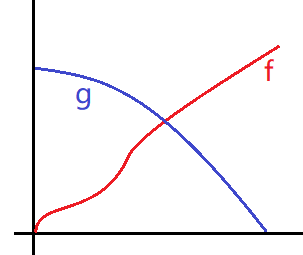
求两个函数的和的 。蓝色的 会不断右移。

可以发现， 右移时，取得最大值的 也只会右移，不会左移。

设 取得 的位置为 。

对于 ，对于 ：

若 即 。

由于 上凸，有 。

将前面的不等式加上 得 即 ，和 为最优解的前提矛盾。

这就证明了决策单调性。注意 指原来的 数组，选择新物品的个数 则不一定有单调性。

在每一层的每一个同余类中使用决策单调性分治，复杂度为 ，可以通过。