CF19E Fairy

题意：给出一张无向图，求删除一条边后此图变成二分图的所有方案。

，时限 。

---

本题数据范围较弱，但存在线性做法。

考虑二分图的充要条件：不存在奇环。

若原图本就为二分图，显然随意删除都可行。

否则，图中存在奇环，我们需要删一条边破坏图中所有的奇环。

显然，答案是所有奇环的交集中的边。

但是，奇环的个数可能非常多，不可能实际求解交集。

---

接下来的思路受到 P4151 [WC2011]最大XOR和路径 的启发。

一个自交的奇环必然引出一个简单奇环，所以我们只需要考虑简单环。

对于图中的一个连通块，先求出任意一个生成树，然后查看非树边。

此时容易处理只含有一条非树边的环，且每条非树边恰好对应一个这样的环，我们把这种环叫做本原环。

树边

若某条非树边形成的本原环是奇环，则这条边是坏边，否则是好边。

对于一条非树边，称其本原环中的树边被其覆盖。

• 引理 1：答案边 被所有坏边覆盖

  考虑每个坏边形成的奇环，显然。

• 引理 2： 答案边不会被好边覆盖。

  

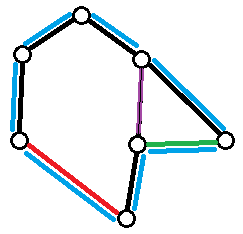
  （图中黑色为树边）

  证明：（反证）一条答案边（紫色）肯定被某条坏边（绿色）覆盖。

  然而，该坏边和好边（红色）的本原环异或并一定能组成一个奇环（蓝色）。

  原因 ： 奇环 + 偶环 - 消去两次的公共部分 = 奇环

  这个奇环一定不包含刚才提到的答案边，矛盾。

• 结论：不被任何好边覆盖，且被所有坏边覆盖的边，就是答案边。

  证明：对于某个简单环，将其中所有非树边的本原环进行异或并，能得到它本身。

  若非树边中有奇数个坏边，则形成奇环，否则是偶环。

  对于一条不被任何好边覆盖的边，其在异或并中是否出现取决于坏边对其覆盖的次数。

  若改变被所有坏边覆盖，则在此时恰好被覆盖奇数次，总是被包含在异或并中。

---

根据结论，容易想到如下算法。

我们统计只含有一条非树边的奇环数量，设为 。

对于坏边，则将其覆盖的边 ，好边则将其覆盖的边 。

最后边权为 的边即为答案。

朴素的链加处理方法——树上差分需要求 ，复杂度带 。

但是，注意到我们进行操作的是非树边，在 的过程中，所有非树边都是返祖边，所以容易 实现差分。

非树边

若 ，则可以删除唯一的一条坏边，否则坏边不可删除。

复杂度可以做到 。