我出的（有趣）高考数学题

发表于 更新于 分类于 阅读次数：

小孩子不懂事出着玩的.jpg

不超纲，无强算。

  • 难度参考

    • 1：萌萌哒课本例题

    • 2：高一高二练习册题

    • 3：高三数学科组能轻松解决的题

    • 4：做出来会被同桌夸数学好的题 / 在晚自习辅导中被提问最多的题

    • 5：可能让重点班全军覆没的题，只有少数几个家伙会做，但在考场上不易实现

    • 6：逆天

注解：此处的难度综合了 思维难度/运算推理的复杂度（按考场时间标准）。部分数据基于同学反馈。

客观题

  • P1 双曲线 与抛物线 有四个交点，它们都在圆 上，则 的半径为（）

    【难度：3.5】

  • P2 已隐藏

  • P3 对于一个多边形，在其内部（含边界）画出一条最长的线段，称为该多边形的直径。一个边长为 的实心正四面体在垂直向下的阳光（可视作平行光源）下自由转动，在水平地面上投下多边形影子 。记 的面积为 ，直径长度为 ，下列选项正确的有

    的最大值是

    若 ， 的最大值为

    若 ， 的最小值为

    【难度：4】

    Bonus： 的最大面积是多少？（这可以单独出一道填空题，但也许太难了）

  • P4 ，下列选项正确的有

    单调递增

    ，方程 至多能有三个解

    若 没有过 的切线，则

    若正项等比数列 满足 ，则

    【难度：5】

  • P5 无解， 的范围为（）。

    【难度：4.5】

  • P6 双曲线 上有一动点 ，， 与 交于另一点 ， 与 交于另一点 ， 的取值范围为（）。

    【难度：5】

  • P7 实数 满足 ， 的取值范围为 （）。

    【难度：3.5】

  • P8 ，（1）， 取值范围为 （）。

    （2）， 取值范围为 （）。

    【难度：4.5】

  • P9 ，则 的取值范围为 （）。

    【难度：4.5】

  • P10 ，，下列选项一定正确的是

    （参考数据：）

    【难度：5】

客观题答案

P1 解答：答案为 。

设四个交点为 ，它们同时满足方程 ① ， ② 。

② ① 得 ，即为过 的圆方程。配方得 ，半径为 。

注解：曲线系思想。（本题有其他做法但计算量较大）

P2 解答：已隐藏

P3 解答：答案为

正四面体内部最长线段长度为 ，投影后，影子内最长线段不会大于 ，A 项正确。

正四面体有四个顶点，影子的形状为三角形或（凸）四边形。对于三角形，直径为最长的边，对于四边形，直径为最长的对角线。 一定时， 取最大值时是等边三角形或正方形，对应面积为 或 （较大），B 项正确。

沿对边中点连线方向投影，影子即为正方形， ，C 项错误。（根据 AB 选项，这也是最大的影子面积）

当 时，有某条边平行于地面，讨论两个面受光和一个面受光的情况，发现某一面垂直地面时 取得最小值，即为 ，D 项正确。

注解：比较考验耐心和空间想象力，慢慢做是不难的。

P4 解答：答案为 。

，A 正确。

记 ，，只有一个零点 。

有2个单调区间，至多 2 零点； 至多 3 个单调区间，至多 3 零点。由图不难构造 3 个交点，B 正确。

没有过 的切线，C 错误。

。若 ，则 ，。

高斯求和得 。

由单调性， 时，求和小于 ， 时，求和大于 ，D 正确。

注解： 是经典的构造。

P5 解答：答案为 。

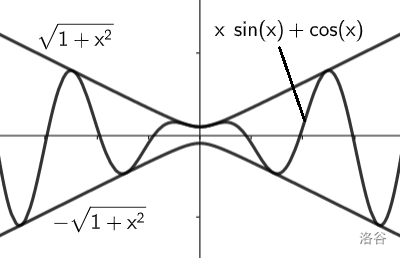
由合一公式 ，故 时无解。

考虑 是否能取等，合一得 （ 类似）

其中 。若要取等，，取 得 ，即 。

该方程有解，故可取等。由图知 时原方程有解。

P6 解答：答案为 。

设 ， 方程为 ，。

与 联立得 ，。

代入 整理得 （其中 ）

代入 整理得 ，即 。由对称性 ，代入整理得 。

关于 轴对称。由 排除相切， 排除顶点，最终取值范围为 。

注解：难以直接化简 的表达式，需发现 对称的性质。

P7 解答：答案为 。

令 ，则 代入整理得 。

，代入消去 得 。

其中 ，易得取值范围为 。（最小值的取等条件是 ，而不是 或 的对称位置）

注解：对于轮换对称式，用 换元，得到关于 的偶函数，无 项，可消去孤立的 。

P8 解答：答案为（1） （2）。

设 ， 能对应回一组 当且仅当 （基本不等式）。

（1）条件即 ，，又 。

观察图像知， 最小值为 ， 范围为 。

（2）条件即 ，，又 。

观察图像知， 最小值为 ， 范围为 。

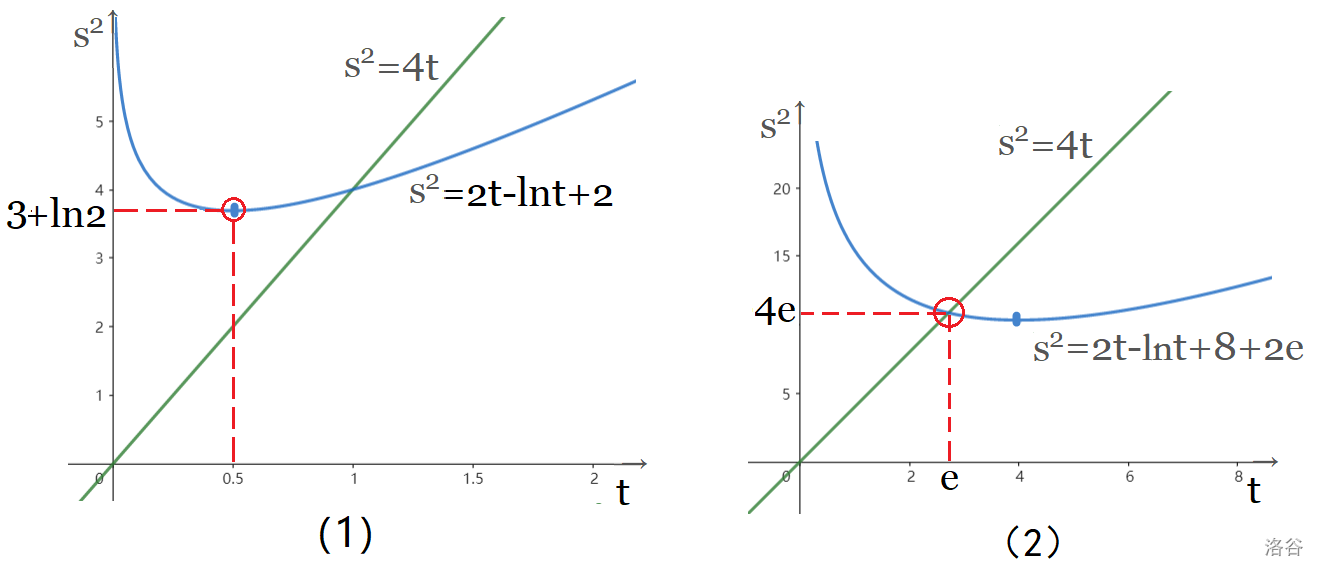
注解：根据原式的形式，不难想到把 换元，但这种换元不是双射。（大多数人用基本不等式做，由于思维不严谨很难拿全分）

P9 解答：答案为 。

先解决一个子问题，，求 的取值范围（用 表示）。

平方得 ，即 。

记 ，则 ， 。

由 ，易知 最小值为 ，最大值为 。

依题意取 ，，即为最小值。

注：也存在不错的几何法。

P10 解答：答案为 。

记 ，显然 单调递增。

A 选项：。

设 ，，由 易知 在 递减，在 递增。

则 ，A 正确。

B 选项： 趋近于 时 趋近于 ，B 错误。

C 选项：。

最大值为 ，C 正确。

D 选项：由 C 知 ，则 。D 正确。

解答题

  • P1 。

    （1）记 ，求 的最小值。

    （2）存在 使 对于 恒成立，求 的取值范围。

    【难度：4.5】

  • P2 中，。

    （1）求 的取值范围。

    （2）若 为锐角，且 ，求 的可能取值。

    【难度：5】

  • P3 在数列 中，记前 项和为 ，，。

    （1）求 的通项公式。

    （2）数列 满足 。 对 恒成立，求正整数 的最小值。

    【难度：5】

  • P4 抛物线 ，点 到 的最短距离为 。

    （1）求 的标准方程。

    （2） 为 上两动点，以 为直径作圆交 于另两点 。证明：存在点 使得对于所有点 ，直线 在 轴上截距为定值。

    【难度：3.5】

  • P5 椭圆 ，，过 的直线与 交于 ，与 轴交于 。记 的外心为 ，求 的取值范围。

    【难度：5】

  • P6 。

    （1）求证： 恰有一零点 。

    （2）若对于任意满足 的 ，均满足 ，求 的取值范围。

    【难度：4】

  • P7 恰有两零点 。

    （1）求 的取值范围。（2）求 的最小值。

    【难度：5】

  • P8 ， 有两个解 ，求证 。

    【难度：5.5】

  • P9 已知圆 ，抛物线 ，直线 与圆相切于点 。 与 交于点 ，过 作 的（除 外的）另一条切线 ，过 作 的另一条切线 ， 交于点 。求证： 在定直线上。

    【难度：5】

  • P10 存在 使 在 时恒成立，求 的取值范围。

    【难度：5.5】

解答题答案

P1 解答：

（1），注意到 ，下证 。

由 ，。

时 ， 时 ，故 ，则 的最小值是 。

（2）① 。 取 ，，符合题意。

② 。，与 矛盾。不存在符合题意的 。

综上所述， 的取值范围为 。

注解：过程很短，但猜的成分很大。通过 上的导数，可以用鞍点法预谋（2）分类的标准（ 的范围以及 最大时 的取值）

P2 解答：

（1）记原式为 ，。

由正弦定理 ，由余弦定理 。

由 ， 。设 ，。

由 得 ，。

时，， 单调递增； 时，， 单调递减；

。 取值范围为 。

（2）

（解法一）试证 ① ，由正弦定理即 。

由 ，，。由 ，整理得

即 ，由 ，① 式成立。

于是 则 即 。

由 ，可知 ，故 。

（解法二）代入余弦定理化简得 ① 。

由 ，，由正弦定理 ，代入余弦定理整理得 。

时 ； 时经验证也满足。

在 ① 中代入消去 整理得 。

由 知 ，代入消去 得 ，故 。

注解：取 猜出 。解法一中配凑成齐次式再证明，解法二中可以预判到因式 。

P3 解答：

（1）① ，② ，② ① 整理得

。

时 。记

由 ， 时 ，故 。

① 中令 得 。令 得 。也符合 。

综上， 的通项公式为 。

（2）设 ， 恒成立。

时

， 可取 。

，故 不符合题意。 的最小值为 。

注解：某些地区这类技巧教得比较多，难度可能要降一档。

P4 解答：

（1）设 上一点为 ， （其中 ）

其对称轴为 。若 ，其最小值在 时取得 ，舍去。

若 ，其最小值在 时取得 ，解得 或 （舍去）

方程为 。

（2）设 。

，同理 。

由 四点共圆， 为直径，。

代入整理得 ，对 同理。

同时满足方程 ，其即为 方程。

令 得截距 对所有 为定值，则 ，解得 。

时 ，或 时 。

注解：本题解法很多，做出来不难，但简洁的做法可以节省大量时间。

P5 解答：

设 方程为 （由题知 不为 ， 存在），令 得 。（）

符合椭圆 方程 ① 与 方程 ② 。

① ② 得 ③ ，代入知 符合 ③。

在直线 上， 符合 ④ 。

符合 ③ ④ 即 。

（或书写：其 系数为 ， 系数为 ， 系数为 【此处 系数和常数项不需要】）

其即为 外接圆的标准方程。则 。

，，其取值范围为 。

注解：利用曲线系思想得到外接圆方程，其中构造了一条斜率相反的直线。

P6 解答：

（1） 定义域 。 单调递增。

；，则 恰有一零点 。

（2）设

① ，则

由 则 。 时 单调递增，

即 ，与 相加整理得 ，由 单调递增， 则 ，符合题意。

② ，则 .

时， 单调递减。

时， 即 ，取 ，满足 但 ，舍去。

综上， 的取值范围为

注解：拐点偏移，构造函数法需证（ 时），端点值 , 再证 ，端点值 ，需 ，可得 。（端点效应）

P7 解答：

不妨设 。

（1）设 。易知 ， 的零点与 的解相同。

， 在 分别单调递增， 至多两解。

① 。 时 ， 无解。 时至多一解，舍去。

② 。； 。故恰存在 。

； 。故恰存在 。故 恰有两解。

综上， 的取值范围为 。

（2）设 。

由 的单调性， 在 分别单调递增。

，故 为奇函数。

由 (1) 知 ，则 与 同解。

时解 易得 。

另一方面，设 。

单调递减； 单调递增。

时，，即 。

由 为奇函数，以 代 得 时 。

则 ，则 。

综上， 的最小值为 。

注解： 等经典构造都可以通过指对换元变为奇函数/偶函数。利用对称性进行切线放缩，可以大大简化计算。

P8 解答：

引理（易证）： 时 ， 时 。

定义域 。 ，由 ， 单调递增。

，不妨设 ，由 单调递增，。

由 ， ，又 ，则 。

设 。由 ， 单调递增。

； 。故 在 上取值范围为 。

取 满足 。

根据引理， 时 ， 时 。

则 。

记 ，则 。

代入得 ，两式相减得 (*)。

，由 且 。

则 即 ，由 单调递增， 即 。

结合 (*) 式， ，则 。

注解：起手用飘带拟合，比较逆天。后面都是对简单分式的处理。

P9 解答：

记原点 ，由 与 切于点 ， ，则 。可得 方程为 。

以 为原点，相同坐标轴方向建立新坐标系。在新坐标系中：

得 。

设 ，则 。

设 ， 方程 即

由 与圆 相切得 即

即 。

对于 同理。可得 满足二次方程：

可得 ， 过 ，原坐标系中 过 。

注解：将原点移动到 与 轴交点，可消去 中常数项，便于后面的因式分解。

P10 解答：

设 ，。

记 ， 单调递增，，。 恰有一零点 。

设 ，。 时 ， 单调递增。故 。

另一方面，取 ，。

单调递增，又 ，故 时 ， 单调递减； 时 ， 单调递增。

此时 ， 可取 。

综上， 的范围为 。

注解：没学过竞赛不等式，也许有高妙做法。