题意:给出一个字符串 。
定义函数 为 的每个后缀与 的 之和。
询问 次,每次给出 ,求 。
,时限 。
后缀 的 即为后缀树上 两点 的 。即 先不考虑 ,单看
,这是 Luogu4211
[LNOI2014]LCA。这对本题有启示。
考虑 的一个祖先 ,其返祖边的贡献系数。在
P4211 中,贡献系数是
子树内 内的点数。即 而在本题中,。贡献系数是 子树内 内的点数。
也即 注意这里考虑的是未压缩的后缀树。
利用 可得
可以拆成 分别计算。
模仿 Luogu4211 将点 到根的链上加一,然后查询 到根的链上,深度不超过 的点权和。
转到压缩后缀树上计算时有一些细节。
使用树链剖分,复杂度是 。
后者可以看作计算
到根的链上深度不超过
的部分每个点 子树中 内的点数。
把树重链剖分,一个询问中符合条件的 会被分到 条重链上计算。
对于一条重链,参与贡献的
在重链顶的子树中,而重链顶子树大小和是 的。
对于询问 ,考虑一对 能贡献的条件。
①
②
设 与重链的 为 ,等价于 。
③
设 与重链的 为 ,等价于 。
④
即
我们把满足条件 ① 的点对
变成二维平面上的点 。
对于询问 ,就是要计算矩阵
以内的点数。这就是二维偏序了。
然而,满足 ① 的点对
可能很多,不能暴力加入,考虑观察这些点对的性质。
对于一个 ,满足条件的 是一个前缀() 。转化成
之后,则是一条斜线(上连续的若干整点)。
而前面说了, 的总规模是
的,那么需要加入的斜线条数也是这个量级。
问题完全转化成了这些“斜线”的二维偏序,如图。
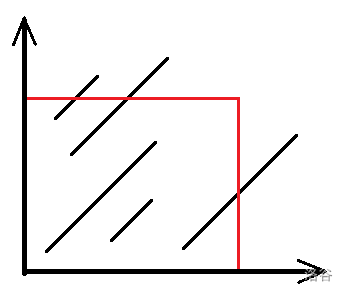
把斜线段拆成两条斜射线的差。我们可以断言,一条斜射线必然穿过限制矩形的右侧(蓝色)或者上侧(绿色),如图。
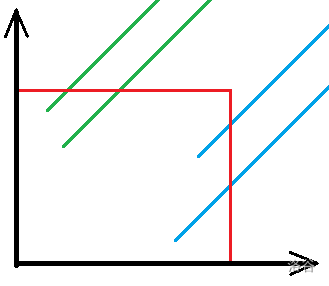
对于穿过右侧的斜射线,其在矩形内的长度为起始点 坐标与右边界 坐标的差。
对于穿过上边界的,则和
坐标有关。考虑分别统计。
若矩形右上角为 直线
与 的交点会是 。
若 则与右侧相交。区间求和即可。需要维护 坐标和以及起始点个数。
对于与上侧相交的情况,翻转坐标系处理即可。
总复杂度 。
代码实现较为复杂,我写了整整一天……

