Uoj#575 【ULR #1】光伏元件

题意：给出一个 的 矩阵 ，表示当前地图上光伏元件的放置情况。 表示位置 没有元件， 表示位置 有元件。

给出代价矩阵 ，表示改变每个位置所需的代价，若为 则表示不可更改。

对于每个 ，给出 。

要求第 行和第 列的元件个数都在 之中，且相差不超过 。

求满足上述要求的代价最小的放置方案。

保证存在合法方案，，，时限 。

---

且

要求第 行和第 列的元件数恰好相等。且不在乎费用，只需要任意一种合法方案。

考虑使用（上下界）网络流来求解。

把行和列分别用点表示，对于位置 ，从行 向列 连边。

• 要求一定无元件：不连边。

• 要求一定有元件：，流量上下界都为 。

• 可以改变，且初始时无元件： 连边容量 。

• 可以改变，且初始时有元件：

  • 连边容量 。
  • 连边容量 ，表示退流。

如何限制行和列的流量相同呢？

可以发现，行的流量是流出的，列的流量是流入的。可以使用循环流的思路来限制，让列 的流量流回行 。

如下图：

求上下界循环可行流即可。

最小费用循环可行流。

对于位置 ：

• 要求一定无元件：不连边。

• 要求一定有元件：，流量上下界都为 ，费用为 。

• 可以改变，且初始时无元件： 连边容量 ，费用为 。

• 可以改变，且初始时有元件：

  • 连边容量 ，费用为 。
  • 连边容量 ，费用为 ，表示退流。

图中可能有负环，需要采用一些技巧。

一般情况

把中间的“循环”边改成这样的设计。

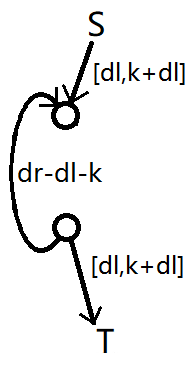
不难发现，由于上下边的下界均为 ，能保证各自至少有 的流量。即行、列元件的个数至少为 。

只需证明 的情况。如图：

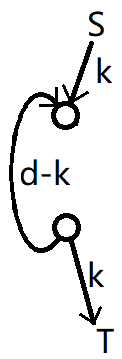
假设上方的流量为 ，下方为 ，中间为 。

那么上点的流量为 ，下点的流量为 。

显然 的差不会超过 ，且 。

反过来，任给出一组合法的点流量 ，我们让中间的边流 。

若 ，则中间的边流了 。

由于 ，余下的流量 和 均 ，能够被两侧的边装下。

若 ，不妨设 ，则中间的边流了 。

余下流量为 ，由前提约束有 。

费用流的实现

点数为 ，边数为 ，流量总量为 。

若采用一般的 SSP-SPFA 费用流，复杂度为 ，原始对偶（Dijkstra）可以做到 。由于跑不满，两者都可以通过。