CF1149C Tree Generator™

题意：给出一棵以括号序列描述的树。

支持交换两个括号（不一定相邻，保证交换后仍为一棵树），回答交换后的直径长度。

，时限 。

---

括号序可以视作有进有出的 dfs 序，其中 ( 代表向下进入某个节点，) 代表向上离开某个节点：

• 结论：设 的 dfs 序小于 。选取 之间的括号，全部匹配对消完毕之后，剩余的括号形如 ))))(((。

  剩余括号个数即为 。（可以给括号加权，此时 是剩余括号权值和）

  证明：先观察 dfs 到达 点时， 的两个括号可能的状态。

  • ① 均填完： 不是 的祖先或子孙。
  • ② 均未填： 不是 的祖先。
  • ③ 只填写了左边： 是 的祖先。

  

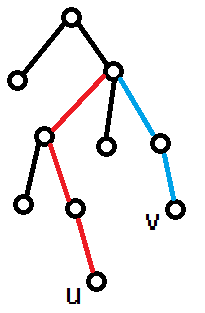
  考察三类边对应的括号：

  边的类型	在 之间留下的括号
  左侧的黑边	无
  之间的黑边	一对（且总是配对）
  右侧的黑边	无
  红边	一个右括号
  蓝边	一个左括号

  红蓝两种颜色恰好拼成 两点间的路径，也恰好对应未消除的括号。

根据以上结论， 就是答案。

---

给 ( 赋权 ，给 ) 赋权 。记 为括号序列第 项的权值。

一段括号序列对消完毕之后，总是形如 ))))((((，我们称右、左括号之间的位置为“分界线”。设分界线前面的和为 (负数)，分界线后面的和为 ，则剩余括号个数为 。

若我们选择的不是实际的分界线，答案一定更劣（依赖于权值非负），所以，问题可以放松为 也就是相邻的两段区间和的差的最大值。

---

考虑用线段树维护。每个节点记录：

• 区间和
• 最小后缀 ，最大后缀
• 最小前缀 ，最大前缀
• 左侧完整（贡献为负），经过分界线，右侧贴右端点的最大值
• 右侧完整，经过分界线，左侧（贡献为负）贴左端点的最大值
• 左右侧均贴端点的最大值
• 区间内部的最优答案

讨论拼拼乐可以转移，复杂度 。

觉得费脑子可以直接 DDP，然后化简矩阵，不过估计也挺麻烦。