Luogu5284 [十二省联考2019] 字符串问题

发表于 分类于 ， ， 阅读次数：

题意：给出一个字符串 ，指定 的两类若干个子串 。

有 组有向支配关系 ，表示 支配 。

求一个字符串序列 ，满足任意一个 都与某个 串相同，设 。

对于相邻的 ，都要满足存在一个被 支配的 串，为 的前缀。

求该字符串序列的最大长度总和，或指出可以无限长。

，时限。

注意到对字符串序列的要求只会涉及到相邻的两个串，很像“路径”。我们可以将其抽象为这样的图论问题：

对每组支配关系，连边 。若 是 的前缀，则连边 。

给 赋权 ，要求出一条路径使得经过的点权和最大。

先解决子问题：

给出一张有点权的有向图,求出一条路径使得经过的点权和最大。

若图不是 DAG，则长度可以达到 。否则，在 DAG 上（拓扑排序）DP 即可。

接下来的问题是如何建立这张图。

支配关系是输入给出的，并不多，可以直接连边。而前缀关系可能有很多，我们需要优化建边。

不难发现，在后缀树上，祖先节点表示的串是儿子节点的前缀，那么 就应该向子树内的所有 串连边。

那么我们使用（外向）后缀树优化建边，就能实现每次连边到一颗子树了。

  • 结论：反串的 的树就是原串的后缀树。

建立后缀树之后，还要在上面定位子串，方法和 相同：从某个前缀节点开始向上跳，直到 区间包含该子串为止。利用 的单调性，不难使用倍增优化。

首先把每个子串定位好，然后从上到下连边,跑个拓扑排序……诶怎么过不去样例?

注意，我们手中的后缀树是压缩的。也就是说，每个点不仅仅表示一个字符串，而是压缩前后缀树中，不分叉父边上的所有串（蓝色部分）。如图：

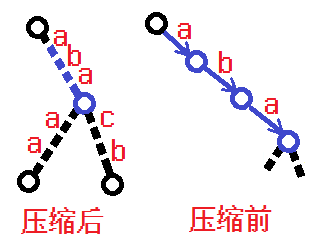
而这条蓝色的边内部也是有顺序的！排在上面的才能转移到下面，逆着来是不行的。

所以，我们对于每个点内部，还要排序+二分来区别顺序。注意到长度短的点在上面，可以按照长度为序。

复杂度 。（认为 同阶）