数论函数求和（上）

发表于 更新于 分类于 ， 阅读次数：

本文共约 8000 字。

Key Words：积性函数，狄利克雷卷积，莫比乌斯反演，gcd 卷积，线性筛，整除分块，整除差分，狄利克雷前缀和，快速卷积性函数

基本概念

  • 数论函数

    • 数论函数：定义域为正整数的函数。

    • 完全积性函数：若数论函数 满足 ，则称为完全积性函数。

    • 积性函数：若数论函数 满足 ，则称为积性函数。

显然完全积性函数是积性函数。对于积性函数，有 ，本文只讨论满足 的积性函数。

  • 熟悉的完全积性函数

  • 积性分解

    对于积性函数 ，给出质因数分解 。则有 推论：只需质数幂处的取值，就足可以确定一个积性函数。

由积性的定义易证。

  • 狄利克雷卷积

    两个数论函数 的狄利克雷卷积为一个新的数论函数，记作 。定义

例如 积性和狄利克雷卷积是本节最基本的两个结构，其重要性堪比钢筋和混凝土。对于初学者而言他们可能很陌生，无论如何，请尽快熟悉。

  • 狄利克雷卷积的运算性质

    • 交换律：。

    • 结合律：。

    • 单位元：记数论函数 满足 。对于任意数论函数 ，都有 。

以上性质根据定义容易证明。

  • 狄利克雷卷积逆

    两个数论函数 满足 ，则称 互为逆元。

狄利克雷卷积的计算

  • 引理（约数/倍数个数和）

    对于每个 ，枚举其在 中的倍数（或因数），复杂度为 。

证明：枚举倍数：总枚举次数 ，近似于 倍调和级数 。

枚举因数：在“枚举倍数”中， 的倍数枚举到 ，当且仅当 是 的因数，两者枚举次数相同，均为 。

  • 乘法的计算：给出 的前 项，计算 的前 项。

    直接用定义式计算。为了方便，可以转枚举因数为枚举倍数。复杂度 。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    #include <cstdio>

    void mul(int *f, int *g, int *h, int n) {
        // 计算 f,g 狄利克雷卷积的前 n 项, 存入 h 中.
        // h 初值为 0. 
        for (int x=1; x<=n; x++) 
            for (int y=1; x*y<=n; y++)
                h[x*y] += f[x]*g[y];
    }

    int main() {
        int N = 8,
            f[N+1] = {0, 1, 4, 5, 2, 7, 6, 3, 8},
            g[N+1] = {0, 3, 1, 6, 7, 2, 8, 4, 5},
            h[N+1] = {0, 0, 0, 0, 0, 0, 0, 0, 0};
            
        mul(f, g, h, N);
        
        for (int i=1; i<=N; i++)
            printf("%d ", h[i]);
        
        return 0;
    }

    /* ----- output: -----
    3 13 21 17 23 55 13 59
       ------------------- */

  • 乘法逆元的计算：给出 满足 ， 满足 ，求 的前 项。

    显然有 。假设对于 已求出 ，欲求 ，有如下递推式

    复杂度 。

    在实现时，也可以转枚举因数为枚举倍数。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    #include <cstdio>

    void inv(int *f, int *g, int n) {
        // 计算 f 狄利克雷卷积逆的前 n 项, 存入 g 中.
        // f[1]=1, g 初值为 0.
        g[1] = 1;
        for (int x=1; x<n; x++)
            for (int y=2; x*y<=n; y++)
                g[x*y] -= g[x]*f[y];
    }

    int main() {
        int N = 8,
            f[N+1] = {0, 1, 4, 5, 2, 7, 6, 3, 8},
            g[N+1] = {0, 0, 0, 0, 0, 0, 0, 0, 0};
            
        inv(f, g, N);
        
        for (int i=1; i<=N; i++)
            printf("%d ", g[i]);
        
        return 0;
    }

    /* ----- output: -----
    1 -4 -5 14 -7 34 -3 -56    
       ------------------- */

积性的保持

积性函数和狄利克雷卷积是本节最重要的两个概念，它们有如下的密切关系。

  • 定理（狄利克雷卷积的积性）
    • 两个积性函数的狄利克雷卷积仍是积性函数。
    • 积性函数的逆仍是积性函数。

证明：

（定理一）设有两个积性函数 ，令 。

设 满足 。

第二行，由于 ，满足 的 只有一对，可以从 中分别提取属于 的素因子而得到。

第四行，我们使用 的积性，将函数值拆开。

（定理二）设有积性函数 ，它的逆是 。设 满足 ，欲证 。

使用归纳法。当 或 为 时，显然成立。假设我们对 的 都已经完成了证明，根据求逆计算式可得

除此之外，常见的函数运算还有点积和复合。

  • 点积：两个数论函数 的点积为一个新的数论函数，记作 。其满足

  • 复合： 给出数论函数 ，其中 的值域为正整数，两者的复合 记作 。

对于积性函数 ， 与 都是积性函数。这不难用定义证明。

一个常见的特例： 是完全积性函数。 是积性函数 都是积性函数。

莫比乌斯反演

抽象的长篇大论令人口干舌燥，在上一小节中没有引入任何一个具体的积性函数！现在到了尝尝具体例子的时候，我们隆重介绍：

  • 莫比乌斯函数

    将 的狄利克雷卷积逆元记为 ，称作莫比乌斯函数。

    即 ，展开得

根据“积性函数的逆是积性函数”， 是积性函数。这是我们要着手研究的第一个“真正有趣的”积性函数。

可以用前文的求逆法 算得 的前 项，但这一做法是保守的，并不能将我们引导向更多的知识。后面我们会看到，有更好的方法取而代之。

为了进一步了解性质，尝试写出 在质数幂处的取值。回忆积性分解的推论，只需质数幂处的取值就能完全确定一个积性函数，所以，这是研究积性函数的通用方法。

根据 ，可得

  • 对于 ，，归纳可证得 。

综上，总结出一般公式 的素因子数目不含平方因子其他

线性筛

线性筛可以在 的时间内求出 以内的素数，并对于合数给出其最小素因子。

其算法流程如下：

  • 枚举
    • 若 没有标记，说明 是质数，将其加入质数集合
    • 从小到大枚举 ，记
      • 标记
      • 记 的最小质因子为
      • 若 ，退出循环
  • 定理：线性筛会标记每个合数恰一次，且得到其最小素因子。

证明：若 被标记，根据退出循环的条件， 中没有比 小的质因子， 是 的最小质因子。

可以发现我们枚举的是 是的最小素因子。记 为 的最小素因子，合数 有唯一的方法拆成 ，，故每个 一定恰被标记一次。

线性筛常用于求积性函数的前缀值。以 为例，记 为 的最小质因子，则有 这样，根据最小质因子，可以递推求出 的前缀值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <cstdio>

const int MaxN = 1000005;

int p[MaxN], totP, minP[MaxN], mu[MaxN];
bool flag[MaxN];

void sieve(int n) {
    // 求出 n 以内的素数，对于合数给出其最小素因子
    // 求出 mu[1] ~ mu[n] 
    mu[1] = 1;
    for (int i=2; i<=n; i++) {
        if (flag[i] == false) {
            p[++totP] = i;
            mu[i] = -1;
        }
        for (int j=1; j<=totP; j++) {
            int t = i*p[j];
            if (t>n) break;
            flag[t] = true;
            minP[t] = p[j];
            if (i%p[j] == 0) break;
            mu[t] = -mu[i];
        }
    }
}

int main() {
    int N = 20;
    
    sieve(N);
    
    auto print = [](const char *note, int *a, int n) -> void {
        printf(note);
        for (int i=1; i<=n; i++)
            printf("%d ", a[i]);
        printf("\n");
    };
    print("Primes: ", p, totP);
    print("  minP: ", minP, N);
    print("    mu: ", mu, N);
    
    return 0;
}

/* ----- output: -----
Primes: 2 3 5 7 11 13 17 19
  minP: 0 0 0 2 0 2 0 2 3 2 0 2 0 2 3 2 0 2 0 2
    mu: 1 -1 -1 0 -1 1 -1 0 0 1 -1 0 -1 1 1 0 -1 0 -1 0
   ------------------- */

对于其他更复杂的积性函数 ，也许不能仅用最小质因子来递推，需要额外记录最小质因子的次数（容易求）。

记 为 的最小质因子， 为 中 的次数，则必有 预处理所有质数幂处取值之后，可以递推。

以内质数的幂的个数为 所以，若求单个 的复杂度不超过 ，则总复杂度是线性的。

  • 例题 4.2.1. 「Coprime Box」

    维护一个正整数集合 ，支持如下三个操作：

    • 向 中加入 。
    • 从 中删除 。
    • 给出 ，求 。

    给出 ，保证 ，操作总个数为 。

    。

Solution：

首先介绍常用技巧：拆解 。（又称为“反演动机”）

  • 引理：

根据该引理： 这样， 的限制就分离了。

回到例题，将询问中的 拆解可得

记 ，如果我们维护了 ，回答询问时只需要枚举 的因数，复杂度 。

记 ，插入和删除相当于对 的单点修改。如果对 加一，则对于所有 ， 都要加一。这样的复杂度也是 。

总复杂度 。

注：如果保证每个数字只出现一次，复杂度 。

整除

接下来，我们将由狄利克雷卷积自然地引导出整除，并介绍针对整除进行计算的方法。

整除分块

  • 例题 4.2.2. 「整除求和」

    给出 ，求下列式子的值 。

Solution：下面我们将给出一个解决该问题的算法，称为整除分块算法。

  • 引理

    对于 ， 的本质不同的取值只有 个。

证明：当 时，至多有 个（显然）；

当 时，，不同的值也至多有 个。

注意到 的单调性，这些取值是一个个连续段。下图是 的情况，分为 个段。

整除分块

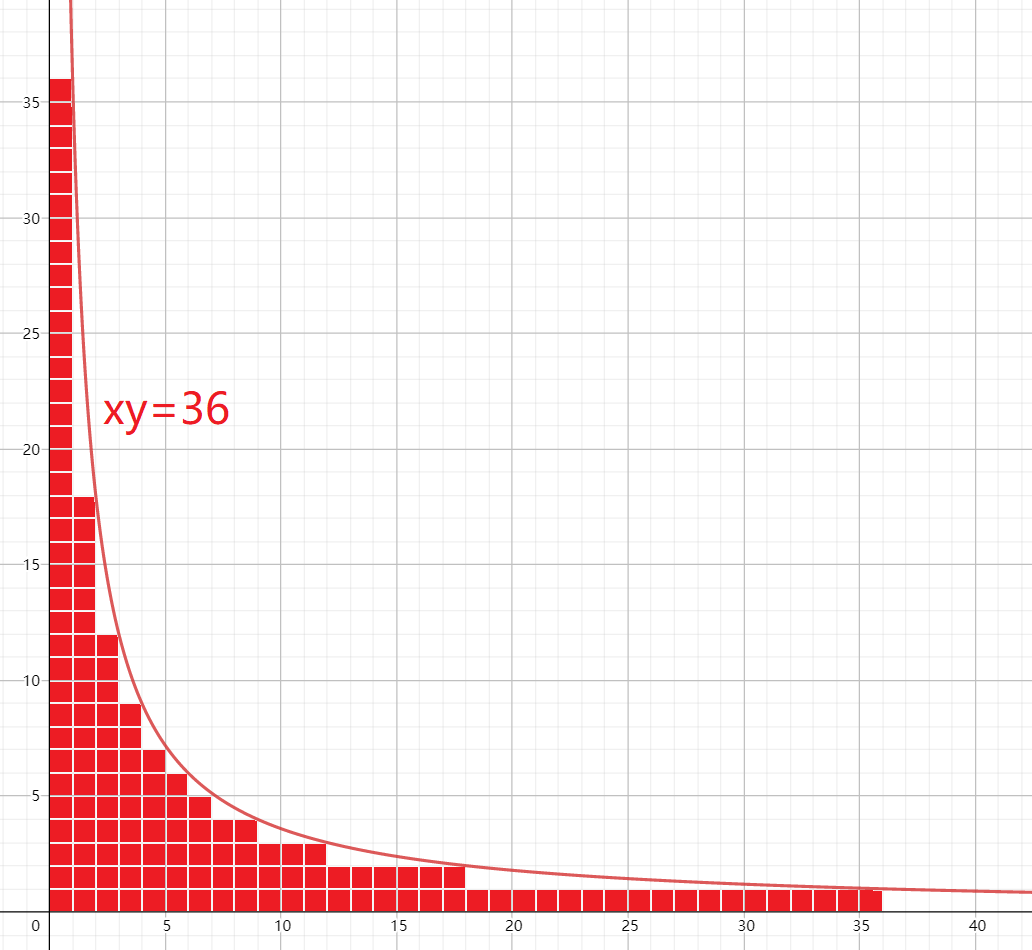
考虑如何快速计算 所在连续段的末尾，即最大的满足 的 。记 ，相当于要求 解得 ，记为 。数学工作完成，接下来可以用如下算法找出所有段，并进行本题所需的求和。

  • 声明变量 ，令 ，当 时继续循环。
    • 记 ，得到一个等值连续段 。
    • 令 加上 ，即这一段的总和。
    • 令 为 ，前往下一段。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <cstdio>

using ll = long long;

ll calc(ll n) {
    ll ans = 0, l = 1;
    while(l<=n) {
        ll r = n/(n/l);
        // 找到一个连续段 i = l~r, 满足 n/i 不变
        ans += (n/l)*(r-l+1);
        l = r+1;
    }
    return ans;
}

int main() {
    ll n = 1e10;
    printf("%lld", calc(n));
    return 0;
}

/* ----- output: -----
231802823220
   ------------------- */

现在你已经对整除分块有了基本的认识，它所揭示的结构是相当重要的。接下来，我们来看看它和莫比乌斯反演是怎样初次走到一起的，它们的经典之作是：

  • 例题 4.2.3. 「Coprime Matrix」

    给出 求下列式子的值 多组数据，，。

Solution：

该和式中出现了整除，且有两个被除数。 形成 个等值段， 形成 个等值段，故 形成 个等值段。

具体算法如下：

  • 声明变量 ，令 ，当 时继续循环。
    • 记 即最近的分段点，得到一个等值连续段 。
    • 令 加上 ，即这一段的总和。其中需要预处理 的前缀和以计算部分和。
    • 令 为 ，前往下一段。

复杂度为 。（ 视为同阶）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <algorithm>
#include <cstdio>

using ll = long long;
const int MaxN = 1e7+5;

int p[MaxN], totP, mu[MaxN], Smu[MaxN];
bool flag[MaxN];

void sieve(int n) {
    mu[1] = 1;
    for (int i=2; i<=n; i++) {
        if (flag[i] == false) {
            p[++totP] = i;
            mu[i] = -1;
        }
        for (int j=1; j<=totP; j++) {
            int t = i*p[j];
            if (t>n) break;
            flag[t] = true;
            if (i%p[j] == 0) break;
            mu[t] = -mu[i];
        }
    }
    for (int i=1; i<=n; i++)
        Smu[i] = Smu[i-1] + mu[i];
}

ll calc(int n, int m) {
    ll ans = 0;
    int l = 1;
    while(l <= std::min(n, m)) {
        int r = std::min(n/(n/l), m/(m/l));
        ans += 1ll*(n/l)*(m/l)*(Smu[r]-Smu[l-1]);
        l = r+1;
    }
    return ans;
}

int main() {
    sieve(1e7);
    
    int T;
    scanf("%d", &T);
    
    while(T--) {
        int N, M;
        scanf("%d%d", &N, &M);
        printf("%lld\n", calc(N, M));
    }
    
    return 0;
}

/* ----- input: -----
5
100 1000
10000 100000
100000 1000000
1000000 10000000
10000000 10000000
   ------------------ */

/* ----- output: -----
60854
607939918
60792862853
6079271166871
60792712854483
   ------------------- */

整除与差分

针对单个“被除数”计算答案时，可以采用整除分块。当我们需要对被除数为 都计算答案时，独立地分别计算是不优的，充分利用前缀信息（即差分，考虑相邻两者的变化）可以得到更好的算法。

观察相邻被除数在差分时的表现，有：

  • 定理（整除的性质）

    ，且此时 。

证明：

  • 时： 恰好整除， 会向下取整，导致 。
  • 时：设 ，则 ，故 。

  • 例题 4.2.5.

    对于（正整数）序列 ，若 ，则称这个序列是好的。

    对 ，分别求值域为 的好序列个数。

    。（无需考虑输出耗时）

Solution：记值域为 的好序列个数为

若对每个 分别使用整除分块，复杂度为 ，无法通过。

对答案数组 进行差分，有

线筛 之后，记 ，则 。

复杂度 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <cstdio>

const int MaxL = 2e6+5, mod = 1000000007;

int powM(int a, int t) {
    int ans = 1;
    while(t) {
        if (t&1)
            ans = 1ll*ans*a %mod;
        a = 1ll*a*a %mod;
        t >>= 1;
    }
    return ans;
}

int p[MaxL/8], totP, mu[MaxL], idk[MaxL];

void sieve(int n, int k) {
    mu[1] = idk[1] = 1;
    for (int i=2; i<=n; i++) {
        if (idk[i] == 0) {
            p[++totP] = i;
            mu[i] = -1;
            idk[i] = powM(i,k);
        }
        for (int j=1; j<=totP; j++) {
            int t = i*p[j];
            if (t>n) break;
            idk[t] = 1ll*idk[i]*idk[p[j]] %mod;
            if (i%p[j] == 0) break;
            mu[t] = -mu[i];
        }
    }
}

int ans[MaxL];

int main() {
    int N, L;
    scanf("%d%d", &N, &L);
    sieve(L, N);
    
    for (int i=1; i<=L; i++)
        for (int j=1; i*j<=L; j++)
            ans[i*j] = (ans[i*j] + (idk[j]-idk[j-1])*mu[i]) %mod;

    for (int i=1; i<=L; i++) {
        ans[i] = (ans[i]+mod) %mod;
        ans[i] = (ans[i-1]+ans[i]) %mod;
    }
    
    int hash = 0;
    for (int i=1; i<=L; i++)
        hash = (hash + (ans[i]^i)) %mod;
    printf("%d", hash);
    
    return 0;
}

常见积性函数

  • 完全积性函数
    • 　　　　　.　　
    • 　　　　　　　.
  • 积性函数
    • 的因数个数
    • 的因数的 次方和
    • 中与 互质的数的个数

欧拉函数

  • 定理：欧拉函数是积性函数。

证明：用 拆解 ，再整理成卷积形式

由此可得 ，则 是积性函数。

接下来考虑欧拉函数的计算，根据定义不难得到

记 ，积性分解并用上式代入，可得

记 为 的最小质因子，则

此式可用于线性筛。

  • 例题 4.2.6. 仪仗队（简化版）

    给出 ，求

    。

Solution：

不难发现这是【例题4.2.3】的子问题，但现在 提供了新的办法

注意到求和是对称的，可以将 的和翻两倍并减去对角线（仅 有贡献），能凑回原答案。这类“容斥”是常见的。

这一结果无疑更加简洁，只需筛出 就能得知答案。问题在于，这是“全新”的吗？ 的组合意义是一种无可替代的观察吗？答案是否定的。

根据【例题4.2.3】的最终结果 我们之前在此处停止，因为这已经可以整除分块。另一方面，我们还不认识 （尤其是其积性），也还了解整除差分的技巧。现在我们可以继续前进，记 ，差分可得

我们仅通过机械的公式推导发现了 就是 的前缀和。

通过标准化（往往是代数化），足够强大的系统理论可以代替观察力。

除数函数

根据定义可知 特殊地，约数个数函数 ，可以视作 。

显见 ，故 是积性函数。

接下来考虑除数函数的计算。对于 ，有

记 为 的最小质因子，有：

则需要动用一般化的线性筛。

再重申一下前面已经知道的小结论

高维变换

在前面的四个小节中，我们从积性和卷积出发建构了较为完善的分析体系。在这一节，我们将揭示“整除”本质上是无穷维偏序，进而说明莫比乌斯反演和其他领域的联系。

唯一分解与高维点表示

记 为从小到大第 个质数。根据唯一分解定理，正整数 可以唯一地分解为素数幂的乘积 。 可以表示为无穷数列 ，记 。

可以将数列视作高维点，根据高维点的偏序，定义 等。

  • 高维点视角下的整除关系

    • 。
    • （逐位取 ）
    • （逐位取 ）

  • 偏序求和

    对数论函数 ，定义

    • 约数求和：

    • 倍数求和：

  • 偏序差分

    定义约数差分 满足 ，即“约数求和”的逆操作。类似地定义倍数差分 。

约数差分与倍数差分统称为莫比乌斯反演。

以高维点的视角来看，约数求和是高维前缀和，倍数求和是高维后缀和。两者的计算都容易通过枚举倍数（因数） 完成。

（根据转置原理）将上述两个算法的影响倒序恢复，即可得到计算约数差分、倍数差分的算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void Lsum(int *f, int n) { 
    for (int x=n; x; x--)
        for (int y=2; x*y<=n; y++)
            f[x*y] += f[x];
}
void Rsum(int *f, int n) {
    for (int x=1; x<=n; x++)
        for (int y=2; x*y<=n; y++)
            f[x] += f[x*y];
}
void Ldif(int *f, int n) { 
    for (int x=1; x<=n; x++)
        for (int y=2; x*y<=n; y++)
            f[x*y] -= f[x];
}
void Rdif(int *f, int n) {
    for (int x=n; x; x--)
        for (int y=2; x*y<=n; y++)
            f[x] -= f[x*y];
}

  • 约数差分、倍数差分与 的关系

    • 约数差分：。

    • 倍数差分：记 ，则

证明：

（约数差分）易知 ，那么逆操作就是卷 。

（倍数差分）

（法一）观察 ，其含义是多重集容斥：先加上全集，再减去含一个质因子的，减多了，再加上含两个质因子的，再减去含三个质因子的，以此类推。对于 ，将下标统一除以 即等价。

（法二）

gcd 卷积

给出函数 ，记两者的 “ 卷积” 为函数 ，满足：

下面给出一个计算 卷积的算法。

先求出 ，然后倍数差分即可得到 。观察 的表达式

尤其注意 ，这条结论很常用。

只需计算 ，点乘之后就是 。

如果你了解位运算卷积，注意到 是按位取 ，可以联想 卷积，有类似的结论。

四变换的快速计算

我们已经知道，如果将正整数质因数分解后视作高维点，约数求和与倍数求和分别可以看做高维前缀和与高维后缀和。高维前缀和相当于对每一维依次做前缀和。于是，对每个维度（质数）逐个做前缀和，即可计算因数求和。

1
2
3
4
5
6
void Lsum(int *f, int n) {
    for (int k=1; k<=totP; k++)
        for (int i=1; i*p[k]<=n; i++)
            f[i*p[k]] += f[i];
            // i*p[k] 是 i 沿着维度 p[k] 向外走一步的点
}

复杂度为 。类似地，也可 计算约数差分，倍数求和/差分。前文提到了许多需要计算四变换的题目，这个技巧可以优化它们的复杂度。

快速卷积性函数

给出数论函数 与积性函数 的前 项，计算 的前 项。

首先将 分解为若干个只和单个素数 有关的函数的卷积。记： 其他 即 只在 处有值，其余为 。可以发现 其中 对应狄利克雷卷积。

正确性不难理解， 能够得到 处的所有值，可以进一步推广到不交的质数集合卷积的情况。在第六小节提出贝尔级数之后，可以更明显的看出，目前的分解就是将每个素数对应的因式单独构造一个数论函数。

综上，我们将卷一个积性函数转化为了卷 个只和单个素数相关的函数。把这些函数分别卷到 上去，就能得到答案。假设我们要由 计算 ，考虑变化量： 需要对 枚举 的倍数计算贡献。对于单个质数 ，复杂度为 总复杂度为 。