多项式的计算(上)
本文约 14300 字。
Key Words:多项式乘法,加法卷积,分治乘法,单位根,点值,插值,线性算法,快速傅里叶变换 FFT,快速数论变换 NTT,复域压缩优化,多项式泰勒展开,牛顿迭代,多项式全家桶(初等函数),分治 FFT,半在线卷积,全在线卷积,拉格朗日插值,多项式多点求值,多项式快速插值
多项式乘法
多项式
对于有限数列
,形如 的函数称为多项式。
用
多项式乘法是多项式计算的基础,其快速算法的重要性不言而喻。接下来,我们将关注有限多项式的乘法问题。即:给出
朴素算法
根据
为了方便书写,我们认为
两侧同时提取
这阐明了多项式乘法对应的数列运算。
卷积
某二元运算
的定义域和值域均为 ,数列 的“ 卷积”为一个新数列 ,满足
不难发现,多项式乘法对应系数数列的“加法卷积”。容易
1 | void mul(int *A, int *B, int *C, int n) { |
列竖式是手动计算加法卷积的一种简便方法,具体操作如下
分治乘法*
不妨设
将
类似将
(将
只需分别计算出
一种显然思路是分别计算
一种巧妙的思路是计算
则
这样可以转化为
1 | using Poly = vector<int>; |
该示例大量使用了
,常数开销大,仅便于理解,实用性较差。
求值-插值法
点值 将多项式
视为函数,对于常数 ,记 为 在 处的点值。 插值 只知道
的若干点值,求出 的系数序列。
多项式插值相当于解线性方程组(即“待定系数法”),根据线性代数知识,还原一个
为了理解点值的性质,看看下面的例子:
多项式乘法的检验
给出
,判定是否有 。
随机一个常数
若
我们已经见识了点值的妙用:通过选定具体的常数,将复杂的多项式乘法“浓缩”为数的乘法。基于这一思想,可以另辟蹊径,设计多项式乘法新的算法框架。
- 第一步:选择足够大的
,选定 个不同的数 - 第二步:求出点值
与 - 第三步:根据
得到 - 第四步:插值求出
的系数
通过求值和插值,我们将多项式
对于一般的
单位根
复数
令虚单位
满足 ,形如 ( )的数为复数。 复数的三角表示
将复数
看做平面直角坐标系中的点 ,记 ,称 为 的模长,射线 与 轴正半轴的夹角 称作 的幅角。有 。 棣莫弗定理(复数乘法的几何性质)
两个复数相乘,模长相乘,幅角相加。
证明:设两个复数为
则
根据正弦、余弦的和角公式,
(如果你是初中生,也可以用 两点间距离公式 / 相似 证明)
本原单位根
次本原单位根记为 ,它满足 互不相同。 。
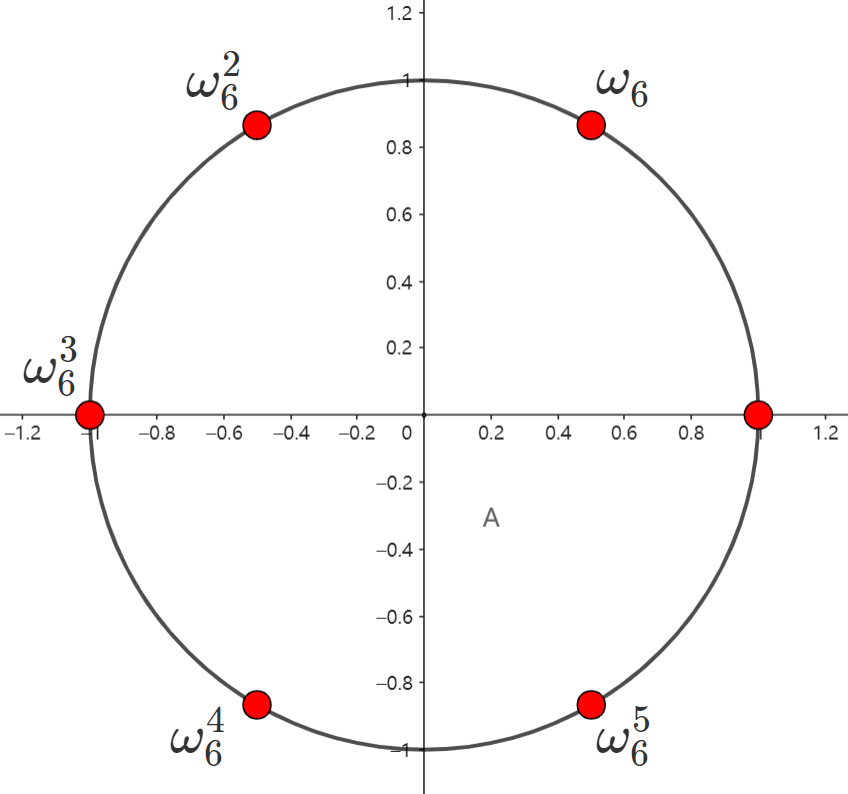
- 单位根的性质
互不相同 (推论: ) (一般情况: )
根据几何性质,不难理解它们。
快速傅里叶变换 Fast Fourier Transform
我们将利用单位根补完“求值-插值法”的框架:
- 第一步:选定
个数 (由单位根的性质,这些数互不相同) - 第二步:对
求出点值 与 (这一步称作 DFT) - 第三步:根据
得到 的点值 (这一步称作点积) - 第四步:插值求出
的系数 (这一步称作 IDFT,即 DFT 的逆过程)
为了便于分治,考虑
DFT
给出
考虑分治,将
假设我们已经知道对
使用分治,复杂度递推式为
为什么是奇偶拆半而不是左右拆半?这本质上是整除
DFT 的线性性与 IDFT
接下来先引入线性算法的概念,再说明 DFT 是线性算法,最后对线性算法求逆得到 IDFT。
线性算法
线性算法的输入为数列
,输出为数列 。算法有一个内秉的系数矩阵 ,算法负责计算
记
根据线性代数知识,线性算法相当于“向量乘矩阵得到结果向量”,记作
线性算法的线性性
对于线性算法
在具体应用中,常利用 DFT(IDFT)的线性性减小常数。
观察
现在让我们暂时忘掉多项式,将 DFT
视作“输入一个数列,输出一个数列的算法黑箱”。我们希望求出其逆算法,而这归根结底是寻找逆矩阵,有结论
证明:
记
记
若
若
综上
我们已经得到了可行的 IDFT 算法,如何快速计算?注意到
欲对数列
构造多项式
实现方法一:将单位根的定义修改为
实现方法二:注意到
至此,我们成功补完了“求值-插值法”的大框架,实现了
1 | const double Pi = acos(-1); |
DFT 的常数优化
- 单位根复用
注意到
此外,我们用到的单位根只有
- 蝴蝶变换和按层迭代
观察分治树,整个计算过程可以分为两步:
- 第一步:反复执行“奇偶拆半”,将
- 第二步:从下往上计算,利用两个儿子的信息计算出父亲的信息。
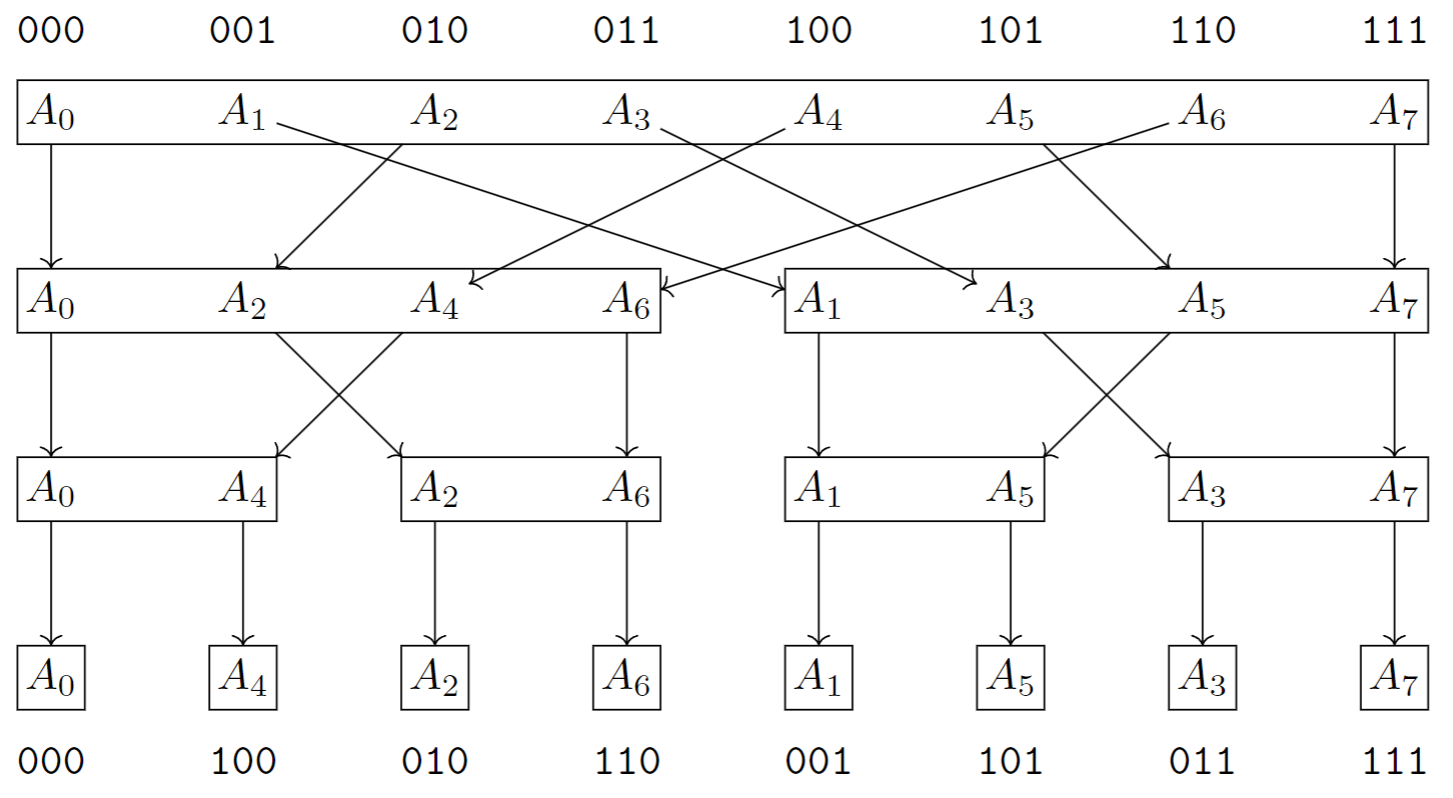
第一步的流程如上图。记
对于第二步,原有的递归算法涉及到大量
优化后的代码如下。该实现代码简短,便于记忆,为大部分选手所采用。
1 | const int MaxN = ______; |
复域压缩优化
利用 DFT 算法的性质,可以节约计算 DFT 的次数。
三次变两次
给出
构造复多项式
两次变一次*
复数的共轭
称复数
共轭的性质
复数的运算具有镜像对称性,对于复数
这种对称性允许我们将整个线性算法共轭。
共轭算法的性质
对任意线性算法
将线性算法展开易证。
考虑如何计算
现给出
构造一对共轭多项式
根据线性性,
若要同时计算两个 IDFT,方法类似。
快速数论变换
许多计数题都要求答案对一个较大的整数
答案系数可达到
如果能在同余系中找到一个数,满足单位根的性质,就能绕开复数,直接在模意义下计算多项式乘法了。
在一些非常特殊的模数下,这的确可以实现。例如质数
任意模数多项式乘法:拆系数 FFT
不利用模数的特殊性质。考虑直接先相乘后取模,这需要设计一个精度足够高的多项式乘法。
题目中的系数
将多项式拆成
我们要计算的是
暴力计算需要
还有一种解决方案是三模数 NTT,需要中国剩余定理合并答案,较为繁琐,故不介绍。
例题 6.1.1. 差卷积
给出两个数组
Solution:将
第三个等号改为枚举
转化为加法卷积,将
- 例题 6.1.2. Luogu3723 [AH2017/HNOI2017] 礼物
形式幂级数
本章名为“多项式计数”,是一种通俗的叫法,实际上我们分析的主要是形式幂级数,在实际计算时归为多项式。
形式幂级数的引入
在这一节中,我们将有限项多项式扩展到无限项的情形。首先定义无穷数列的运算。
无穷数列的运算
对于无穷数列
以这些运算为基础,我们可以将(有限项)多项式扩展为(无穷项的)形式幂级数。
形式幂级数
对于无穷数列
形式幂级数的运算
对于形式幂级数
这三个运算的定义和多项式一致。当无穷序列只有有限前缀非零时,形式幂级数退化为多项式。为了分析形式幂级数,可以从其有限前缀入手,这需要引入截断的概念。
截断
两个形式幂级数
截断的性质
对于形式幂级数
这两项性质容易验证。它们说明,如果我们只对形式幂级数的前
形式幂级数和幂级数的区别*
幂级数
对于无穷数列
例如我们熟悉的几何级数
“形式幂级数”和“幂级数”的分歧在于,后者关注无穷求和的取值,而前者关注系数数列。例如对于
未来的章节将关注形式幂级数,因为我们关注系数数列而非无穷级数的和。我们需要关注系数的收敛性,而非整个无穷求和的的收敛性。
例如对于
- 表:形式幂级数与幂级数的对比
| 形式幂级数 | 幂级数 | |
|---|---|---|
| 本质 | 无穷数列 | 函数(无穷求和) |
| 用于标记数列项 | 某个未知实数 | |
| 收敛性要求 | 系数收敛 | 无穷求和收敛 |
形式幂级数的初等函数
从形式幂级数的乘法出发,可以定义一系列初等函数。
- 形式幂级数的幂
- 乘法逆:若
- 有理次幂:若
- 乘法逆:若
先前我们总是将形式幂级数写成逐项求和的形式,例如
“封闭形式”指不含不定求和或不定乘积等的简单形式。它是一种约定俗成的概念,例如“
”暗含了不定乘积,仍被视为一种可接受的封闭形式。
形式幂级数的复合
对于形式幂级数
两个形式幂级数的复合会产生无穷求和,这可能导致收敛性问题。
复合收敛的充分条件
对于形式幂级数
证明:由于
形式幂级数的指对函数
定义形式幂级数
形式幂级数的导数和积分
对于形式幂级数
形式导数
形式不定积分
可以验证上述记号符合我们想要的微积分性质,例如
接下来,我们将给出计算各类初等函数的算法。
乘法逆
给出
- 递推法
对比系数知
边界是
- 倍增法
假设已经计算出
对数函数
给出
设
牛顿迭代法
传统意义上的牛顿迭代法可以求
对于函数
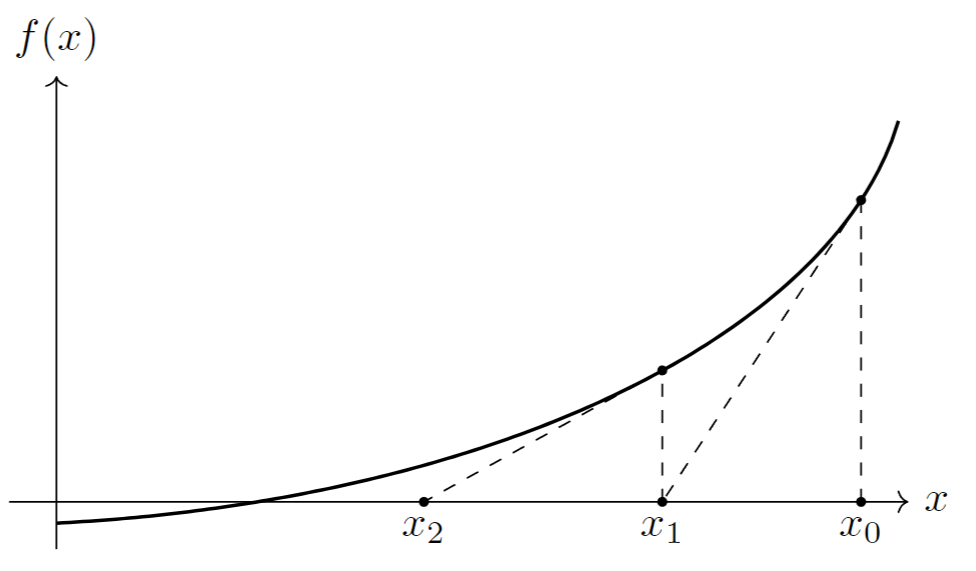
随着迭代的进行,
记形式幂级数的集合为
形式幂级数上的函数
可以令函数
例如
形式幂级数方程
给出函数
例如
一般地,如果
形式幂级数(复合)方程的截断
利用截断的性质易证。我们称
若
证明:先证
记
理论准备完毕,下面介绍如何求方程
欲求
证明:将
由
利用该公式,每次可以将解的次数倍增。其形式和
在计算时需要注意,由于
利用这个结果,再次探究多项式求逆的倍增算法。构造
多项式开平方
给出
构造
假设已求出
复杂度
多项式指数函数
给出多项式
递推法:求导得
将
分离可以得到多项式 的递推方法
倍增法:构造
假设已求出
多项式 k 次幂
给出
使用快速幂计算,复杂度
若
若
当
记
其中
注:实际上这套方法是“整式递推”,更多知识可见后文《递推关系》一节。
多项式带余除法
多项式取模
给出
多项式取模的性质
对于多项式
接下来考虑如何计算多项式取模:给出多项式
如上设
当
分治 FFT
多项式的连乘积
给出
采用分治法,记
分治树有
分式求和
给出
的前
分别维护分子分母,
算得
半在线卷积
类似 DP 优化,使用“中序遍历的 CDQ 分治”,对于当前区间
此时已递归左区间,
到达叶节点
可以分多叉来降低复杂度,假设将当前区间均分成
一个经典的应用是多项式
全在线卷积
为了便于理解,想象一个阶梯状的矩阵,位置
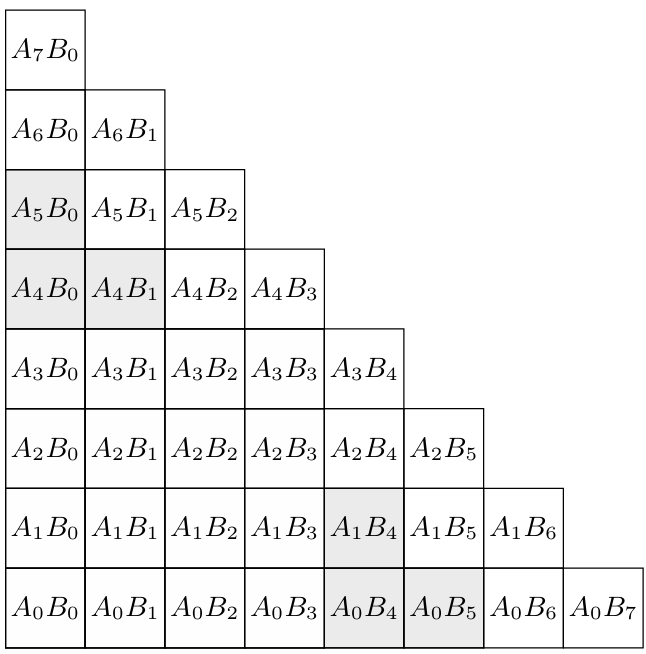
- 记
- 处理
- 若
- 若
- 若
- 调用
例如对于

当到达叶子
- 若
- 若
- 已得到正确的
可以发现,算法不会用到未知的
调用
还有一种等价算法。一个规模为
- 一个规模为
- 一个规模为
- 两个并行的,规模为

复杂度递推式
对于上述两种算法,多叉平衡均可以让复杂度更优。
求值与插值
拉格朗日插值
给出
这相当于解线性方程组
首先证明解唯一。根据线性代数知识,相当于证明系数矩阵
范德蒙德矩阵
称各行为几何级数的矩阵
证
范德蒙德行列式
对于
可以用归纳法证明。
由
接下来尝试构造出解。先解决
对于一般情况,首先对
拉格朗日插值公式
对于互不相同的
- 例题 6.1.3. CF622F The Sum of the k-th Powers
多项式多点求值
给出多项式
- 引理
证明:
记
根据多项式取模的性质,记
于是有如下分治算法:
- 对于分治区间
- 计算
- 计算
- 到达叶子
其中
对
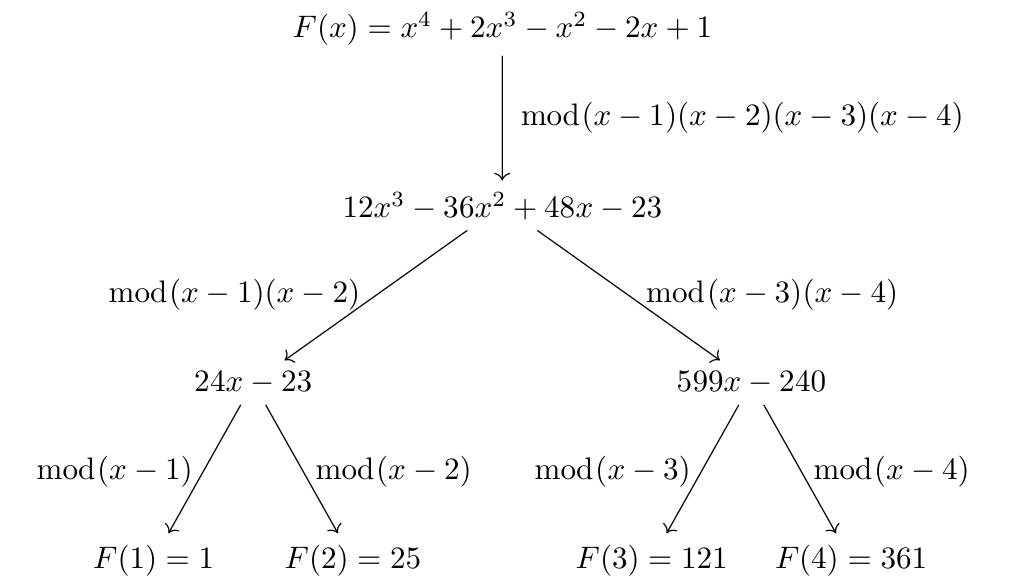
下文《转置原理》一节会介绍一个常数更小、更易实现的多点求值算法。
多项式快速插值
写出拉格朗日插值公式
先对每个
记
记