多项式的计算（下）

发表于 分类于 ， 阅读次数：

本文约 12700 字。

Key Words：拉格朗日反演，转置原理，简易多项式复合，下降幂多项式，Chirp Z-Transform，Bluestein 算法，点值变换，位运算卷积，子集卷积，集合幂级数，高维幂级数

Todo：多元拉格朗日反演

转置原理

前文已经介绍过线性算法的概念，本节考虑线性算法的转置，并阐明一对互为转置的算法之间有何关系。

  • 线性算法的转置

    对于两个线性算法 ，记他们的转移矩阵为 ，若 ，则称 互为转置。

  • 初等矩阵

    以下三种矩阵称为初等矩阵：

    • 将单位矩阵 的第 行交换的矩阵。该矩阵左乘一个向量的效果为，将该向量的第 位交换。
    • 将 从 改为 的矩阵。该矩阵左乘一个向量的效果为，将该向量的第 位乘以 。
    • 将 从 改为 的矩阵。该矩阵左乘一个向量的效果为，将该向量的第 位加上第 位的 倍。

    容易发现，初等矩阵的转置仍然是初等矩阵。具体地：

    • 将向量的第 位交换：转置后不变。

    • 将向量的第 位乘以 ：转置后不变。

    • 将向量的第 位加上第 位的 倍：转置后，将向量的第 位加上第 位的 倍。

  • 转置定理 转置定理给出了互为转置的两个线性算法之间的转化方法。

接下来，考虑如何由线性算法 得到线性算法 。

对于矩阵 ，它可以表示为若干初等矩阵的乘积： 每个初等矩阵对应一次“交换”，“乘加”等操作。在对某个向量执行线性算法时，只需将表示中的初等矩阵逐个左乘上去。

根据转置定理，有 根据 的初等矩阵表示可以得到 的初等矩阵表示。倒序逐乘初等矩阵的转置即可以同样的时间复杂度完成转置算法。

和 能互相转化，这给我们一个启发：如果计算 是困难的，可以先尝试计算 ，成功后，将整个算法转置，就能得到计算 的算法。这就是转置原理的基本思想。

贡献图

可以认为，线性算法维护一个含 个变量的数组，输入初状态，对其不断进行三种基本操作，最终输出末状态。然而实际情况中，算法的变量结构可能很复杂，且有中间变量，难以用线性代数的语言书写。我们需要更合适的刻画工具，为此，引入“贡献图”的概念。

将所有“修改”视为新建。即：修改某个变量时，为它创建一个新的“版本”，同时保留旧版本不删除。下图展示了一个例子： 这会使得所有操作都变为操作三。

建立一张有向图 ，对于操作“变量 加上变量 的 倍” ，连边 ，这样会形成一张有向无环图，因为老变量会贡献到新变量，而新变量不可能贡献到老变量。我们称 为线性算法的“贡献图”，以下是一个例子，省略了边上的乘数：

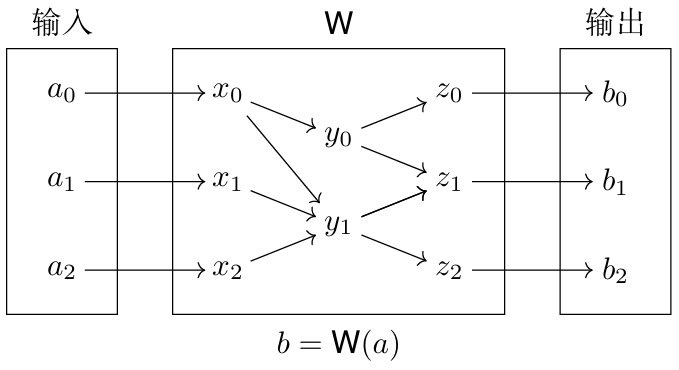
image-20250325145230509

图中的每条边代表一个操作，我们没有说明操作的计算顺序，但可以推断出：计算顺序一定是拓扑序。

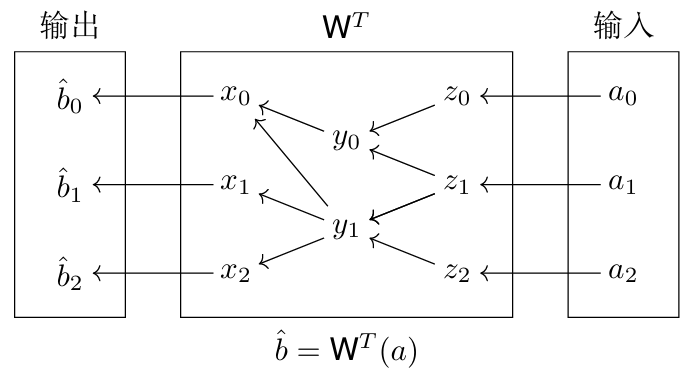
如何对 进行转置？首先将操作顺序翻转，然后根据第三类初等矩阵的转置规则，将每条边的起点和终点交换，不难发现， 对应的贡献图是原来的反图：

有了贡献图，分析转置算法时就方便多了。

DFT 的转置*

仅用于常数优化

DFT 和 IDFT 的转移矩阵是对称的，故它们的转置是其自身。即 尝试将 DFT 的分治算法转置，这样可以得到一种新的计算 DFT 的方法。

原版 DFT 要先 bitrev（将序列编号二进制取反）再计算，转置后的 则先计算再 bitrev。注意到原版 IDFT 需要先 bitrev，两个紧接着的 bitrev 抵消，可以省略。这样可以减小 FFT 的常数。

下面介绍将 DFT 的分治算法转置的具体方法。分治计算时，最小操作单元具有如下形式（见“单位根复用”） 其中 为某常数， 是下一分治层的值。该操作转置后变为 根据转置定理，将所有最小操作单元转置，然后倒序执行即可。同一个分治层内部的最小单元互不干扰，只需将分治层倒序。

加法卷积的转置

数列 进行加法卷积得到 ，其中 若将 看成输入， 看成常量（主导线性算法的转移矩阵），记“卷”为线性算法 ，则该算法的转移矩阵为

考虑其转置算法 ，记 ，则 即为差卷积。

接下来用 表示转置后的多项式乘法。（符号右边的多项式视为转移系数，左边的多项式视为输入）

多点求值

  • 给出 次多项式 和常数 ，对 求各个 。

，将 视为转移系数，记线性算法 对应的矩阵 ，则 。

考虑其转置算法 ，记 ，有

将 构造成多项式： 这是分式求和问题，可以分治 FFT 计算，复杂度 。具体流程如下：

  • 对于分治区间 ，维护分母 与分子 。

  • 将 填写到叶节点 。

  • 自底向上分治，处理 时，记 ：

  • 最终，计算 即可得到答案。

将该线性算法 转置，就得到多点求值算法 。具体流程如下：

  • 与输入（）无关，只和算法的转移矩阵有关，为常量，先用分治 FFT 预处理。

  • 输入 ，计算 。

  • 自顶向下分治，对于区间 ， 的贡献图为 将其转置， 的贡献图为

  • 最终得到的各个 即为答案。

值得留意的是，由于顺序颠倒，在 中，作为输入的 一开始被放置在 处，答案由 给出； 则倒过来了，输入 被安放在 处，答案由 给出。

复杂度 ，相较于传统的分治取模算法，较易实现且常数更小。

拉格朗日反演

基本概念

  • 形式幂级数的复合逆

    对于形式幂级数 ，若 ，且 ，则称 为 的复合逆。记为 。

  • 复合逆的性质

    • 复合逆是对称的，即 当且仅当 。
    • 形式幂级数 满足 ，，则它拥有唯一的复合逆。

证明：

性质一：令 ，。

易知要么 要么 。由 知 即 。

性质二：设 的复合逆为 ，易知 ，对于 有 其中 ，可以解出 。这个递推可以确定唯一的 。

  • 形式洛朗级数

    引入负次数， 称作形式洛朗级数，其中 为有限值。

引入有限的负次数后，幂级数的乘法（数列的加法卷积）仍然容易定义。

原先 的幂级数无乘法逆，若考虑形式洛朗级数，则一切幂级数（除了 ）都存在乘法逆。具体地，记 的最低项为 ，则 有常数项，其乘法逆有定义，故

注：若涉及到负无穷多次项，某些收敛的性质可能失效。

如尝试将 写成封闭形式，若缩写为 ，再展开成 ，显然错误。

一元拉格朗日反演

拉格朗日反演指明了提取复合逆的一项系数的方法，这是为数不多的能从封闭形式中提取系数的方法之一。

  • 引理（形式留数）

    对于无常数项，有一次项的整式 ，有

证明：当 ，，而求导不可能产生 项。

当 ，

此处构造 ，使常数项非零，便于考虑。

  • 引理

    对于无常数项，有一次项的形式幂级数 和任意洛朗级数 ，有

证明：记 ，根据引理

  • 拉格朗日反演

    形式幂级数 无常数项，有一次项，则

    （扩展） 为形式洛朗级数，有

证明：

令 即可得到经典情况。

  • 另类拉格朗日反演

    形式幂级数 无常数项，有一次项，则 （扩展） 为形式洛朗级数，有

证明：

令 即可得到经典情况。

对于另类拉格朗日反演，分歧在于得到 的方式：构造时不求导，而直接将 乘上去。

两者比较，拉格朗日反演的形式简单，便于推导；另类拉格朗日反演证明思路直接，且能处理 的情况。

实际计算时，可以将定理改写成 其中 有常数项，可以求逆。整个计算过程在形式幂级数中完成，无需涉及形式洛朗级数。

  • 例题 6.1.5. 幂的横截

    已知 互为复合逆，给出 。对 分别求出 。

Solution：记 ，目标是 ，使用扩展拉格朗日反演

只需计算 的各项系数，复杂度 。

进一步地，若 没有复合逆，可能有以下两种情况：

情况一， 的最低次项次数 ，记 ，那么 就有复合逆。 只在 时有值，故对 计算幂的横截即可。

情况二，，记 ，，转化为正常情况或情况一。对 计算幂的横截，最后 ，二项式定理展开后可以卷积。

多项式复合

简易多项式复合

  • 右复合

    给出 次多项式 ，计算 的各项系数。

提取系数得

记 ，，则

差卷积计算即可，复杂度 。

  • 右复合

    给出 次多项式 ，计算 。

配方得

  • 右复合 或

    给出 次多项式 ，计算 ， 的前 项系数。

根据 ，有 。只需计算 与一次乘法。

复合 的情形类似。

  • 右复合

此外，我们可以在 的时间内右复合任意二次分式 或任意三次式 ，思路都是将要复合的式子拆成一系列 和一次分式 的复合。这样的手段对五次及以上的一般多项式无效（五次以上方程无根式解）。而且，随着次数增大，时间常数也随之增大，在实践上不如下面的 通解。

参考：

  • 右复合 短有理分式

    给出多项式 以及短多项式 （长度为常数），求 的前 项。

先解决短有理整式，即求 。

可以分治 FFT 解决，对于分治区间 ，记 ，，有分治转移 复杂度 。

若加入分母 ，分别维护分子分母，最后求逆即可。

  • 右复合 （其中右复合 G 容易计算）

    给出多项式 ，求 的前 项。

将 的系数按下标模分类，记 则 代入 得 对每个 分别计算。需要计算 次右复合 以及多项式乘法。

  • 右复合

    给出多项式 ，计算 的前 项系数。

只需要对每个 求出 （甩掉阶乘），记 ，则

分治 FFT 即可。复杂度 。

Bostan–Mori 算法

它的一个更初步的应用是求线性递推的远处项，推荐先学习《线性递推》一节。

Bostan–Mori 算法可用于提取二元分式的一行

上下同乘 得 记 ，注意到 ，故 只有 的偶次幂有系数，可以表示为 。记 ，将 的系数奇偶分类，表示成 ，得 分母只有偶系数，分子奇偶系数分离，讨论 的奇偶性，当 为偶数时只涉及 ，为奇数时只涉及 ，故 每次递归，需要保留的 的次数减半， 的次数加倍，规模近似不变。

递归层数为 ，复杂度 。其中 为初始的 的次数，当 为常数时，复杂度 。

多项式复合

给出多项式 ，，求 。 将其视为线性算法， 视为输入， 视为贡献系数。考虑该线性算法的转置 将 构造成多项式 其中 。

Bostan–Mori 算法可 计算 。将该算法转置，就解决了多项式复合。

多项式复合逆

给出 的前 项，，求 的前 项。

【例题6.1.5】利用复合逆解决了“幂的横截”，结论是 换言之，若求出各个 ，就能得到 的各项系数，计算 次方即得 。

这将目标转化为“幂的横截”，记 ，将其构造为多项式 可用 Bostan–Mori 算法 计算。（这为“幂的横截”提供了通解）

一元多项式的其他常见算法

牛顿级数与下降幂多项式

  • 基

    多项式序列 满足 是 次首一多项式。称这样的一组多项式为基。

例如 就是一组基，称为方幂基。

  • 基表示

    对于任意多项式 和任意基 ，记 的次数为 ，总能找到一个系数序列 使得 这种表示 的方法称作在基 上的表示。

证明：找出 的最高次 ，令 ，然后令 ，这样能使得最高次项变为 。不断重复这一过程即可得到数列 。

我们不仅可以用方幂 ，还可以用其他的基来表示多项式，下面是两种常见的扩展：

  • 牛顿级数

    形如 的多项式称为牛顿级数。

  • 下降幂多项式

    形如 的多项式称为下降幂多项式。

对牛顿级数 使用二项式反演可得 二项式反演可以卷积加速，我们可以在 的时间内在系数 与点值 之间相互转换。

若要计算两个牛顿级数的乘法，可以先转换为点值，让点值相乘，再转换为系数。

对于下降幂多项式，由于 ，两者的系数容易转换。

与普通多项式相转化时，需要快速插值或求值，复杂度 。

  • 例题 6.1.7. 拉格朗日插值2

    给定一个不超过 次的多项式 的 个点值 ，和一个正整数 ，求 。

    答案对 取模，，。

Solution：首先将 的点值转化为下降幂多项式 ，再利用下降幂的二项式定理，计算 的各项系数（与上文“复合 ”方法相同），最后转化回点值 。

Chirp Z-Transform

给出 次多项式 和常数 ，对 求出 。

  • 引理：。

利用该引理，可以构造卷积：

记 ，则 可以差卷积计算，复杂度 。

注：各个 可以两次前缀积计算，避免快速幂，以减小常数。

任意长度 DFT/IDFT：Bluestein 算法

  • 循环卷积

    两个数组 的长度为 的循环卷积是一个新的数组 ，其中

循环卷积等价于 下的多项式乘法。

  • 定理

    长度为 的 FFT 在计算长度为 的循环卷积。

证明：

FFT 计算的是 ，其中点表示点乘。展开得

应用单位根反演 。

即为循环卷积。或对循环卷积定义式进行单位根反演，可以从另一个方向验证。

我们用 FFT 计算多项式乘法时，会“选择足够多的点值”，多于两多项式的次数之和。虽是循环卷积，由于卷积数组够长，实际上没有溢出，和加法卷积等效。

前文的 FFT 算法只能处理长度 的情形（稍加改造可以计算 质因子不大的情况）。如何计算 为任意值的循环卷积？一个朴素的想法是，先计算双倍长度的普通加法卷积，然后再把循环的部分手动添加。这做法的确可行，但没有保留“点值”的性质。我们希望实现任意长度的 DFT/IDFT，而不仅仅是卷积。

注意到 DFT 相当于对 做 Chirp Z-Transform，于是可以 求任意长度 DFT（IDFT 可以由 DFT 得到）。这被称作 Bluestein 算法。

位运算卷积与集合幂级数

点值变换的构想

前文对任意二元运算 定义了“ 卷积”，记其符号为 。我们尝试推广“求值-插值法”的思想，定义 卷积的点值变换（Point value Transform）

  • 点值变换

    二元运算 定义域、值域均为 。

    若存在线性变换 ，使得对于任意数组

    （其中点表示点积）则称 为 卷积对应的点值变换。

点值变换将卷积转化为点积。注意到点乘具有交换律、结合律，若 卷积有点值变换，那么 运算必须要有交换律、结合律。

加法卷积并不满足这里说的“定义域、值域均为 ”，但 FFT 计算的其实是长度为 的循环卷积，其中下标的运算 符合定义。

如何设计我们想要的线性变换？设 为 的变换系数，展开 得

又根据 ，将左侧的 代换掉

对比系数，再由序列 的任意性，可知

我们需要构造矩阵 满足这一条件。而且，为了从点值变回系数，我们还需要 的逆变换 ，这要求矩阵 有逆。

例如，对于长度为 的循环卷积，我们知道 DFT 的系数 ，那么

符合公式。

位运算卷积

先约定一些必要的记号。

  • 位表示

    记位的大小为 （其中 ），将自然数 拆成 的形式，其中 ，则称 为 的位表示。

  • 位运算

    有一系列二元运算 ，其中 定义域和值域为 。自然数 的位表示为 ，计算 ，位表示 对应的数为 ，则称 通过位运算得到 。这种位运算可以记作二元运算 。

定义为了一般性稍显冗杂。实际应用中，多数情况有 （即 进制数），且每个位的运算 规则相同。

例：按位与（）、按位或（）、按位异或（）的位大小均为 ，位内运算 值域均为 。三者的位内运算的取值表为

位运算卷积的点值变换

对于一个（值域有限的）位运算 ，如果我们已经知道其各个位内运算 对应的点值变换系数 （称作位矩阵），则有如下方法构造 卷积的点值变换。

记 的位表示为 ，，构造

由于位运算直接各个位之间互不干扰，易知 符合公式 。

为了从点值变回系数，我们还需要 。

  • 定理

证明：证法和“多元反演”一致。

记 。 故 。

已知位运算 的位矩阵，有如下计算 的算法：

记最高位为第 位，位值域为 ，将 按下标最高位分成连续等长的 段 ，每段抹去最高位独立进行 变换，记结果为 ，则 这实际上是由序列构成的向量 左乘 得到 。暴力计算的复杂度是 ，如果乘矩阵 有快速算法，亦可采用之。

考虑计算的复杂度，在位运算卷积中 ，记总位数为 ，复杂度递推式为 ，得复杂度 。

计算 的方法相同，用 作为系数即可。

经典位运算卷积

记位矩阵为 ，三种经典位运算卷积的构造如下。

  • or 卷积

扩张成完整的变换系数 ，可以发现 。 恰是高维前缀和，相应地， 恰是高维前缀差分。

  • and 卷积

扩张成完整的变换系数 ，可以发现 。 恰是高维后缀和，相应地， 恰是高维后缀差分。

  • xor 卷积 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
const int
    mod = _____,
    inv2 = _____,
    Wor[2][2] = {{1,0}, {1,1}},
    Wand[2][2] = {{1,1}, {0,1}},
    Wxor[2][2] = {{1,1}, {1,mod-1}},
    IWor[2][2] = {{1,0}, {mod-1,1}},
    IWand[2][2] = {{1,mod-1}, {0,1}},
    IWxor[2][2] = {{inv2,inv2}, {inv2,mod-inv2}};
// 三种点值变换的系数矩阵，以及它们的逆矩阵
void FPT(int *A, int n, const int W[2][2]) {
    //根据位矩阵 W 快速计算点值变换
    for (int len=1; len<n; len<<=1)  // 枚举子问题的长度
        for (int p=0; p<n; p+=2*len) // 枚举本问题的左侧起始位置
            for (int i=p; i<p+len; i++) {
                int sav0 = A[i];
                A[i]     = (W[0][0]*A[i] + W[0][1]*A[i+len]) %mod;
                A[i+len] = (W[1][0]*sav0 + W[1][1]*A[i+len]) %mod;
            }
}
void bitmul(int *A, int *B, int *C, int n,
            const int W[2][2], const int IW[2][2]) {
    // 根据位矩阵 W, IW 计算 A 和 B 的位运算卷积。
    FPT(A, n, W);
    FPT(B, n, W);
    for (int i=0; i<n; i++)
        C[i] = A[i]*B[i] %mod;
    FPT(C, n, IW);
}

计算 or 卷积、and 卷积的点值变换的算法称作快速莫比乌斯变换（FMT），计算 xor 卷积的点值变换的算法称作快速沃尔什变换（FWT）。

扩展位运算卷积

将位运算卷积扩展到位大小 的情况。

  • 高维 max 卷积（将按位或扩展为每一位取 max）

构造 为在第 位上做前缀和，。 为前缀差分。

  • 高维 min（将按位与扩展为每一位取 min）

构造 为在第 位上做后缀和，。 为后缀差分。

  • 不进位加法卷积（将按位异或扩展为每一位相加模 ）

在每个位内是循环卷积，若单位根存在，根据 DFT/IDFT，有

子集卷积

将 位二进制数视为大小为 的集合，其中 表示出现， 表示不出现。集合的并相当于取 and，集合的交相当于取 or，集合大小 是 的二进制表示中 的个数。

  • 子集卷积

    定义序列 的子集卷积为 ，其中

这和前文定义的“ 卷积”不太一样， 卷积中每个乘积 都有贡献，而此处只有 的乘积才有贡献。即只考虑集合的不交并，相交则不贡献。

有多少对有贡献的 ？答案是 ，和“枚举子集”的复杂度相同。这说明子集卷积可以暴力 计算。

考虑使用卷积知识加速计算。直接套用前面学习的或卷积只能求 ，无法再满足 。

注意到 等价于 。而 可以用加法卷积来描述。人为增加一个元 ，将 替换为 ，计算或卷积。提取 即为满足 的乘积的贡献。

取 就得到答案。暴力计算关于 的多项式乘法，复杂度 。关于 的多项式称为“占位多项式”。

（子集顺序的）全在线子集卷积

  • 是 的子集卷积。在你正确地对于所有 计算出 后才能得到 的值。计算 。

按照 的顺序计算 ，这样就能保证需要的值已经得到。枚举子集可以做到 。

相当于按照 的次数从小到大计算，将 视为主元，对 逐次计算 。需要计算 次或卷积，利用 PT 变换的线性性，只需 次变换。复杂度仍然是 。

集合幂级数

  • 集合幂级数

    定义 由这样的 构成的形式幂级数称为集合幂级数。

位数为 的集合幂级数也可以定义成有 个元 的多元形式幂级数，每个元 对 取模，这样次数只能是 和 ，相乘也符合规则。

集合幂级数的单位元为 （或写作 ），可视为“常数项”。

容易定义集合幂级数的乘法逆、有理次幂。此外，仍可用无穷求和定义指数和对数： 两者都要求 。

与经典形式幂级数不同的是，集合幂级数有“点值”，也就是点值变换后得到的占位多项式。这为计算带来了很大便利，比如说，若要计算乘法逆，只需将点值占位多项式取倒数，再变换回去。 也类似。由于占位多项式一般较短，此处常用 的递推法。

多元多项式

二元多项式乘法

  • 给出二元多项式 ，， 的最大次数分别为 ，计算两者的乘积 。

记 二元多项式乘法对应二元加法卷积：

考虑如何计算。将 扩大两倍，转化为计算二元循环卷积，这相当于只有两个“位”的位运算卷积。可以发现，先每列做 DFT，再每行做 DFT，就能得到“点值”；点乘后，先每行做 IDFT，再每列做 IDFT，即可恢复为系数。

复杂度 。

多元多项式乘法

  • 我们有两个多元多项式 和 ，希望计算

    记 ，希望得到 的算法。

在高维加法卷积中，由于每一维度上次数都会翻倍，所以实际计算系数总量是 级别的。当 较大时，复杂度不尽如人意。

下面给出一个 计算 元多项式乘法（的截断）的方法。由 一般至少为 ，。

将一组下标 看做位表示（位值域为 ），可以将它们编码为一个自然数，即令

这样就把多维映射到了一维上。

此时，下标 的加法对应着大数 的加法，但要将超出截断范围（产生进位）的贡献去除。

模仿子集卷积，考虑设置一个合适的占位多项式来辅助判定进位，将错误的贡献分流除去。构造占位函数 ，满足：

  • 不进位，则 。
  • 进位，则 。

这样，我们计算二元多项式 的乘法，然后利用第二维去除无用贡献即可。具体地，在 项只保留 系数。

剩下的问题就是找到一个合适的 函数。模仿子集卷积，不难想到 （各位数码之和），但这个函数的值域太大，会导致 的次数很高，不便计算。

令 ，注意到 在第 位进位当且仅当 可以想到令 这样，虽然单个 的值仍然很大，但由于 可知 。只需在 上记录长度为 的循环卷积即可得到所有信息。

在实现时，我们需要计算 ， 的乘法。我们将 设为主元进行 FFT，复杂度是 。得到的“点值”是 的多项式，暴力计算乘法，一次乘法复杂度 ，点积总复杂度 。

多元多项式的求导与牛顿迭代

我们已经把多元多项式乘法转化为二元多项式 的乘法，具体地，每次相乘后在 系数中保留 项。

观察那些被去除的贡献，由于产生了进位，他们分布于比 更低的项，在接下来的运算中，这些贡献没有机会回到 项。由此可见，我们的乘法相当于只维护二元多项式在 上的上轮廓。

我们考虑完整的二元多项式（即每次乘法后不进行去除），以 为主元，可以正常定义其求导和牛顿迭代。牛顿迭代中的运算全部转化为乘法，若只关心上轮廓，可以在计算过程中只保留上轮廓。将 的计算封装后，具体实现和一元的情形非常相近。