组合符号化（上）

发表于 2025-03-27 分类于算法竞赛，知识阅读次数：

本文共约 14500 字。

Key Words：DP 中的卷积，分拆数，贝尔数，解析组合，OGF，无标号组合构造，EGF，二项卷积，有标号组合构造

DP 中的卷积

组合计数 DP 中经常出现加法卷积的形式，此时可以利用形式幂级数解决问题。接下来，我们将观察一系列经典例子，为学习解析组合做铺垫。

卡塔兰数

卡塔兰数满足，时为对括号构成的合法括号序列数。

接下来求的通项公式。

先将组合问题转化为代数形式。对含有对括号的序列，枚举第一对括号包含了多少对括号，可得递归式这是卷积的形式。构造生成函数，则故解得，产生了两个根，其中有一个是我们需要的。

考察常数项，的分子常数项非零但分母常数项为零，是非法的，故舍去。所需的解为。

可提取系数将广义二项式系数化简得

我们运用的分析方法可以概括为“组合递推式加法卷积形式幂级数方程”，下面我们继续探索该思路在组合 DP 中的应用。

背包的合并

记表示物品集合选出的重量的方案数，表示物品集合选出的重量的方案数。

若同时考虑两组物品，的 DP 数组有转移

组合意义：枚举在第一堆物品中拿取的重量，则在第二堆物品中拿取重量。

可以发现这就是加法卷积。构造生成函数则有它们被称为普通生成函数（Ordinary Generating Function, OGF）。

例：有种糖果，每种可以取个，则取个糖果的方案数为

求和只有项。用容斥（枚举一个糖果集合超出限制）可以得到相同的结果。

分拆数

记为将拆分成若干无序正整数的和的方案数，称为分拆数。

例：可以拆分为或或，故。

拆分数可以转化为完全背包问题：每个正整数都可以用任意多次，可以视作重量为的物品做完全背包。

重量为的物品的 DP 数组在（不拿），（拿一个），（拿两个）……是，其余是。对应的 OGF 是分拆数的 OGF 是每个物品的 OGF 之积，即

如何计算的前项？观察分母的展开

发现展开式中大部分项的系数都为，只有少部分项有的系数。经过合理的猜测，可以发现：

五边形数定理

它在次以内只有项，于是可以暴力求逆得到的前项。

后文将指出，对应解析组合中的，并给出一个的计算方法。

染色问题（带标号背包，二项卷积）

用种颜色染一条有个格子的纸带，每种颜色的使用次数有一些要求（如：颜色必须染奇数次，颜色不能染超过次等），求染色方案数。

考虑 DP，记表示颜色集合染个格子的方案数，表示颜色集合染个格子的方案数。

若将两组颜色都用上，的 DP 数组有转移组合意义：选出个格子用染，余下的个格子用染。

该公式和加法卷积非常相似，但携带有二项式系数，故称为二项卷积。将组合数拆开，可以得到加法卷积的形式

数列是和的加法卷积。数列的二项卷积在逐项除以之后转化为加法卷积。

构造生成函数则这些生成函数称为指数生成函数（Exponential Generating Function, EGF），这是因为数列的 EGF 是指数函数。二项卷积对应 EGF 的乘法。

为了方便表述，约定这样能正确提取 EGF 对应数列的系数。

接下来用 EGF 表示本题的 DP。第种颜色对应的数列为 $允许染次颜色$ ，其 EGF 为，答案 DP 数组的 EGF 为为了便于理解，给出两种特例：

例一：颜色没有使用限制

这相当于每个位置随意染种颜色的其中一种，方案数显然为。

再看生成函数的推理，每种颜色的 EGF 均为，则答案的 EGF 为，提取系数得

也得到正确答案。

例二：用红蓝绿三种颜色，染一条有个格子的纸带，使得红色和蓝色的格数是偶数（包括），求方案数。

绿色的 EGF 显然是。

红蓝的 EGF 只有偶数项，即

答案的 EGF 是

提取系数得答案为

连通图计数

个节点的有标号无向图有条可能的边，每条边都可能存在或不存在，故有标号无向图共有种。这其中，有一些图是连通的，求个点的有标号无向连通图的个数。

考虑 DP。记为个点的有标号无向图个数，为个点的有标号无向连通图个数。如题所述，。

设节点编号为，枚举点所在的连通块大小将所有图分类。对于，分别考虑“点所在的连通块大小为的个点的有标号无向图”的方案数，构造可以分为三步：

在点中选出个点，和点组成连通块，记为点集。
连接点内部的边，方案数为（要求连通）。
连接其余点内部的边，方案数为（随意连接）。

故方案数为将它们求和，就能得到所有图：

拆开组合数整理得这是加法卷积，令则多项式求逆即可计算，复杂度。

贝尔数

记为将数字划分为若干个无序集合的方案数，称为贝尔数。

的划分有如下种，故。

贝尔数满足如下递推式

组合意义：枚举所在集合的大小，选出和同集合的个数，其余数的划分方案形成子问题。

将组合数拆开，可得加法卷积的形式

对于右侧，构造，，则右侧是。

左侧怎么处置呢？构造，这样左侧就是。我们想用表示出，这样就能得到关于的方程了。

观察和的对应情况，中的单项式对应到中的单项式，次数减一且系数乘，不难发现这正是求导。于是，则有方程

解这个微分方程，得，其中为常数。要使得这个表达式收敛（即使得无常数项），只有，于是

可以用多项式 exp 计算，复杂度。

解析组合

解析组合试图以一个较为机械化的方式帮助我们将组合计数问题从模型直接转为生成函数。——EntropyIncreaser

符号化组合对象，解救选手于组合意义的地狱之中。——x义x

在上一小节中，我们分析了一系列组合问题，主要是将组合 DP 中的卷积转化为生成函数。

在分析过程中，一些关键的组合结构反复出现，能否用一种系统的方法，从组合结构直接得到生成函数，从而省去复杂的组合/代数推导？解析组合正是我们需要的工具。

基本概念

组合对象

组合对象指满足某一性质的树、图、串等可计数的对象。组合对象组成的集合成为组合类。

对于组合类，其中每个对象都被定义了一个 “大小” ，可能代表节点个数，串长等。

约定使用字体表示组合类，代表空对象，大小为，）

组合对象的拼接

组合对象的乘法被定义为两者的有序拼接，可以记作或有序对。

对于两个组合对象的拼接，定义。

该定义是自然的。例如两个长度为的字符串接起来就得到一个长度为的字符串。

组合类的加法：不交并

若组合类不交，则定义为。

为了书写方便，有时将单个组合对象自动视为集合。

组合类的乘法：笛卡尔积

定义为组合类的笛卡尔积，记作，即为从两个集合中各取一个元素先后拼接形成的集合。

例：若，则。

不难发现这就是计数的“加法原理”、“乘法原理”。

我们已经对组合类（集合，元素有大小）和组合结构（不交并，笛卡尔积等）进行了定义，下面来看两个例子。

01 串

记 01 串的组合类为，将其内容用无穷求和的方式写出：

对于某个 01 串，要么为空，要么是由 0 或 1 开头，接上另一个（可空）01 串而得。

写成组合符号，即

这个式子概括了的组合结构。不过，我们目前尚不能进一步处理它。
有序二叉树（卡塔兰数）

定义有根有序二叉树满足：有根，儿子有左右之分。下图列出了前棵非空有根有序二叉树：

一棵有根二叉树要么为空，要么由“左儿子，根，右儿子”三部分组成。则有：

其中，表示单个节点（根节点）。这个式子概括了的组合结构。

需要特别解释的是，这里的“组合等式”，也就是组合类之间的等式，并不是指“严格相等”，而是指“互为双射”。

例如，左边解释为一棵有序二叉树，右边解释为一个序列（忽略空集）： $有序二叉树节点有序二叉树$ 两者不能直接说成“相等”。但如果我们把有序二叉树连到节点上，就形成了一棵大有序二叉树，构成双射，这就是等号的含义。换一种理解方式，组合方程中组合对象的乘法不一定代表“拼接”，需要我们赋予它与“拼接”同构、且适合语境的组合含义。

组合对象与生成函数

将所有大小为的组合对象集合记作。定义计数序列 ，即大小为的组合对象的总数目。我们的任务通常是求出。

例如：定义为字符集为的字符串集合。定义字符串的大小为其长度。长为的 01 串共有个，则。

如果我们只对感兴趣，即只对组合类的大小感兴趣，不关心组合对象的具体形态（如拼接顺序等），可以做如下简化：将组合对象用形式幂代替，这被称作组合对象的幂表示。

定义组合类的（普通）生成函数为组合对象的幂表示之和也就是计数序列的生成函数。

组合类运算对应着怎样的生成函数运算呢？不难发现：

组合对象的乘法对应幂表示的乘法：

的幂表示为，等于的幂表示之积。
组合类的加法对应生成函数的加法。
组合类的笛卡尔积对应生成函数的乘法：

利用乘法运算律可以验证。

综上，我们有生成函数的基本运算和组合类的“集合加法”，“笛卡尔积”是同构的。我们可以将组合类的构造翻译为生成函数的运算。

上一小节说明了，OGF 的乘法和计数背包的转移（加法卷积）是同构的。因此，我们其实早在学习背包 DP 时就已经熟悉了笛卡尔积的代数形式。

回看“基本概念”中的两个例子，将得到的组合方程翻译为生成函数：

01 串

解得，，即长为的 01 串有个。
有序二叉树（卡塔兰数）

解得，正是卡塔兰数的生成函数。

从组合对象到幂表示

下面来看一个广为流传的，动的“由组合对象变为幂级数”的例子，它对我们的理解大有裨益。我们将首先用特殊的符号写出组合对象，并展示它们一步步简化成的过程。

骨牌密铺

用的骨牌铺满的矩形，有多少种方案？

用表示一个竖着放置的骨牌，表示一个横着放置的骨牌。

的矩形的覆盖方法共有种，分别为目前情况还很友善，只不过是玩玩积木。记为所有铺法的组合类，用无穷求和写出所有的铺设方案如下其中对应什么都不铺。

目前还远远称不上是“幂级数”，只是一种简单的罗列。

定义两种铺设方案的乘法为顺次拼接，如

注意到，对于某种铺设方案，要么是，要么以开头，要么以开头。根据这个分类，能写出：如果允许（形式上）的除法和减法，解方程可得封闭形式上式蕴含了的所有信息，现在我们可以略去不感兴趣的细节来取得我们感兴趣的信息。

比如，我们并不关心具体铺设顺序，只关心使用横竖骨牌的个数，则可以将每种铺设方案拆散，如可以拆成，现在乘法仅仅是无序组合，所以有交换律，同时“幂”也开始出现了。

此时，可以写作其中原来的合并为了。

这里中有对象，可以写成类似幂级数的形式，不过为了简洁偶尔省略括号中的内容。

对封闭形式进行改写，有回忆，将上式展开：能看出：用个竖骨牌和个横骨牌铺设的矩形，方案数为。这其实是直接给出了的所有系数。

进一步地，如果我们不关心骨牌的方向，只关心个数，则用表示个骨牌，将均视作，可得这和斐波那契数列的生成函数非常相似（只差一个因子），现在不难看出。（稍加观察，能得到例题 6.2.6 中的结果）

的含义

关于形式幂级数，总有个老生常谈的问题：中的到底是什么意思？我们总是反复强调“形式幂级数不是函数，不是一个未知的实数”，却很少解释究竟是什么。

有些人可能会回答：“ 什么也不是，只是一个形式上的记号。”这说得通，但有些让人云里雾里。

在学习了组合对象的幂表示之后，我们有了另一种理解：生成函数中的是一个匿名的、具有良好运算律的组合对象，它的求和可以整理成一个形式上的幂级数。如果保留组合对象的“原味”（如拼接顺序等信息），就会退化成更具体（但运算性质更差）的“骨牌”等物件了。

（无标号）组合构造

复杂的组合类往往由其他组合类构造得来，一个构造是从一个组合类映射到一个组合类的函数。

生成函数的定义已经翻译了 “集合不交并”，“笛卡尔积” 这两个最基本的构造。下面让我们继续来看，在生成函数的视角中，各色组合构造会有怎样的形式。

Sequence 构造

对于组合类，定义 “生成不定长序列” 构造为：又作，即用若干中元素拼成有序序列。

此处要求，否则求和不收敛。

翻译成生成函数，有例：

01 串

记。 01 串可以看作 0,1 生成的序列，即。则
斐波那契数列

可以视作用长度为的骨牌铺满的区域的方案数。

记，。则

无标号 Amplification 构造

组合类的“k-膨胀构造”定义为： $共个$

大意是说，中的元素都是中某个元素复读次的结果，你也可以理解成所有元素的大小都扩大倍。

翻译成生成函数，在幂表示中将简单地替换为即可。

置换群下的等价类

组合类中的所有对象都是中若干元素拼接成的序列，即。定义的“容量”为。

令为一个置换群列，其中是一个元置换群。

组合对象在作用下本质相同（等价），当且仅当，这里的置换移动序列中的元素。也就是说，两者序列长度相等，且存在一种置换，将序列换到完全一致，则两者相等。

例：串。

令为全体置换组成的置换群列。记为 01 串的组合类。

在上拆分的结果为，。

由于可以任意置换，可置换成，故和在上等价。

当为全体环置换（循环位移）时，两者不等价。

对于组合对象，定义 $与等价$ ，称其为一个等价类。中元素大小相同，定义等于中元素的大小，即。

定义为将视为的序列后，在置换群类下的等价类的组合类。

例：01 串。

仍记，为 01 串的组合类，为全体置换，有为了方便和直观，我们从等价类中抽取一个（字典序最小的）元素代表。如实际上代表了。

Multiset 构造（完全背包）

令为全体置换组成的置换群列。定义“生成（无序）集合构造”为：

在下，本质相同。

不妨为中的所有组合对象规定一个顺序，只统计字典序单调不降的序列，这样每个等价类恰好被统计到一次（其代表是字典序最小的那个序列）。

于是，按某种顺序枚举中所有对象，并一次性加入若干个，能写出：改写为生成函数，则有或从组合意义 DP 出发，生成无序集合相当于完全背包，也可以得到该公式。

至于计算，尝试取再：暴力完成后面的求和，复杂度是。然后只需计算。

稍作代换可以得到另一个有趣的式子：

记，称为 Polya 指数。记逆变换为。

模板： Luogu4389 付公主的背包

逆变换：Luogu3784 [SDOI2017]遗忘的集合

定义“生成（无序）k-集合构造”为：

考虑引理，记为置换的环大小集合（多重集）。

朴素地计算，置换高达个，效率低下。注意到本质不同的是拆分数级别的，可简化计算。

Cycle 构造

令为全体环置换组成的置换群列。定义“生成（无标号）环构造”为：

为了便于理解，可以将中的元素看作珠子，而中的元素就是生成的项链。两条项链若能通过旋转变得相同则本质相同。

例：01 环的组合类为

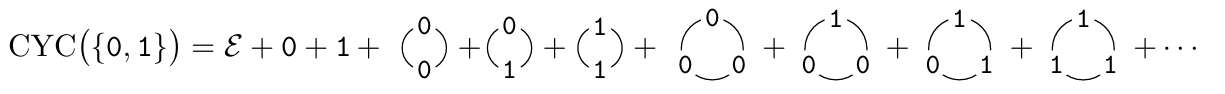
其中

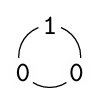
代表等价类

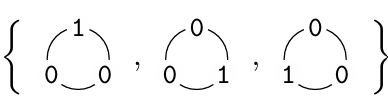
接下来考虑如何将组合式翻译为生成函数。

先分析个珠子组成的环，记该组合类为，生成函数为。

枚举中旋转置换的步数，旋转步会产生个等价类，大小均为。这可以看作有个重复次的珠子，即。

根据 Burnside 引理，置换下的等价类个数等于置换下不动点的平均数，有 Burnside 引理只是一个关于“数目”的结论，所以这里并没有对应的组合式。

对各个求和可得所有环的生成函数若计算前项，中只有个非零项，求和时暴力累加即可，复杂度。

Power Set 构造（01 背包）

定义“生成（无序）幂集构造”为：

即枚举每个元素是否存在。也可以粗略地理解为：。实际上，的组合意义就是背包。

将组合式改写为生成函数，则有：

计算时仍然取再：

求和可以暴力完成，然后只需 exp。

记，称为改版 Polya 指数。记逆变换为。

有标号对象与 EGF

标号的概念

复杂的组合对象可能由更基本的元素构成，如“无向图”由点和边构成。这些组合对象的“大小”常常被定义为所含某种元素的个数，这种元素被称为主要元素，如无向图的大小被定义为其节点数，“节点”是其主要元素。

有些时候，对于组合对象，它的主要元素上面会有标号，形如一个的排列。如果两个组合对象标号对应后不同，则它们不同。对于无标号的情况，主要元素可以任意打乱。

例如无标号无向图和有标号无向图，它们判断相等的方法是不同的：

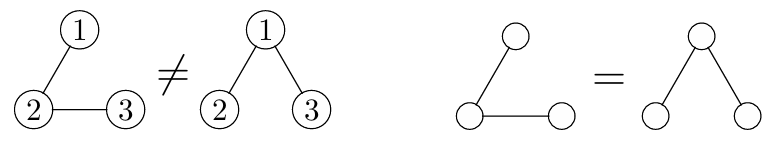
下图展示了所有个点的无标号无向图和有标号无向图。

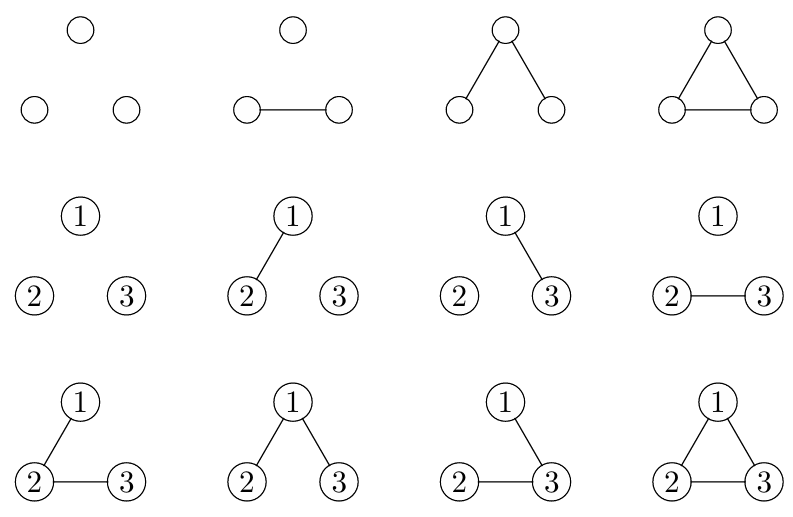
有标号对象的基本运算

我们将从头开始定义“有标号组合对象”、“有标号组合构造”，并将其翻译为生成函数。

对于有标号组合对象，它恰好拥有个“节点”、“格子”等容器，每个容器可以填一个标号，填写的标号为的排列。

考虑有标号组合对象的乘法，即的结合能构造出什么样的组合对象。在无标号计数中，被简单地定义为的拼接，有标号对象的乘法则更加复杂。

考虑两张有标号无向图，我们希望将两张图拼在一起，形成一张新的有标号无向图，可以划分为两个部分，分别对应到。例如：

我们将这一过程称作有标号对象的“归并”。

如上图，有标号对象的归并的方式不止一种，主要是标号的方案不止一种。我们需要将标号集合划分为两个大小分别为的子集，将这些标号分配给。

例如将划分为，然后将其对位赋给，然后将简单拼接，过程如下：

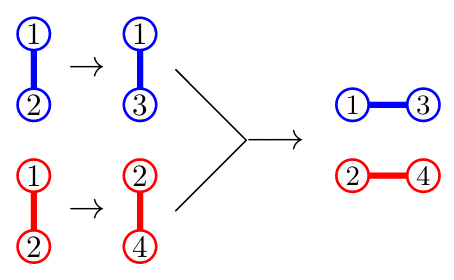
这得到上面产生的第二个图。

划分标号的方案有种。对于的情形，方案有种，对应上面产生的个有标号无向图。

为什么叫做归并呢？考虑两个序列和，我们希望将两者归并成一个序列，使得内部元素的顺序不变，则归并方案数是。下面展示了这种方案：我们将视作“图中标号为 ”的点，类似。归并后的排位对应新的标号，例如中：

排第位，的新标号为。
排第位，的新标号为。
排第位，的新标号为。
排第位，的新标号为。

这样也产生第二个图。

总而言之，两个有标号组合对象的乘积定义为一个集合，包含它们归并产生的所有个组合对象。

进一步地，两个组合类的笛卡尔积定义为不难发现每一项各自不交。

对于有标号组合对象，有设大小为的组合对象的幂表示为，则需满足这也就是前文所说的“二项卷积”，不难发现只需构造

于是，定义有标号组合类的 EGF 为： EGF 的乘积对应有标号组合类的笛卡尔积。

有标号组合构造

有标号 Sequence 构造

“生成序列构造”定义为：或。

要求，否则求和不收敛。

类似无标号的情况

Pointing 构造

组合意义是选择一个元素作为特殊元素（如选择图的根）。就像一些无大小的“贴纸”，贴在对应元素上面。

不难发现，若，则（在个元素中选出一个）。故

置换群下的等价类

“无标号组合构造”中定义了记号，接下来，我们将其沿用到有标号组合构造中。

对于某置换群列和组合对象，令，我们希望由得到。

先考虑中容量为的等价类，记为，对应生成函数。

可以发现，对任意一个序列，因为分到了各异的标号，它们互不相同，故的所有重排都互不相同，等价类大小就是重排方案数，也就是置换的个数。去重时，简单地除去即可，故对求和得

综上可见，在有标号计数中，“除去一个置换群列”是简单的。

Set 构造

记为全体置换组成的置换群列（即允许元素任意打乱），“生成集合构造”定义为：

易知（全体元置换），故

例1：有标号连通图。

记有标号图的集合为，有标号连通图的集合为，则。

翻译为生成函数，，，只需求即可。
例2：贝尔数。

为将标号划分为若干非空无序集的方案数。

记非空集合的组合类为，，（显然，对于任意，大小为的有标号无序集就只有一种），。

记集合划分的组合类为，则，故。

有标号 Cycle 构造

记为全体旋转置换，“生成环构造”定义为：

易知（全体元旋转置换），故

此外，若为全体旋转置换和翻转置换，记可以发现故

有标号组合类的复合

标号无关

定义一个组合类是“标号无关的”，当且仅当：对于任意，将标号任意打乱后得到，仍有。

反之，则称是“标号有关的”。

例如：

令

则是“标号有关”的。
令为有标号无向连通图，则是“标号无关的”，因为打乱标号不影响是否连通。（我们研究的绝大多数性质都属此类）

复合积

现有一个有标号组合对象满足，又有一个序列，记两者的复合为。它是一个组合对象，大小是，含义是：对，将中编号为的元素换成序列中的第个对象，且在上保留注释“”。替换后，本身不再占据大小。

记这一运算称作“复合积”。

例如，令。，则其中得到元素的方式是：

选择；
选择；
将中的标号替换为，标号替换为，同时保留原标号注释，得到。

然而，在实际问题中，我们往往不希望保留上的原标号注释。为了去掉注释，考虑：

复合对象在置换群下的等价类

对于两个复合对象，满足，用全体元置换来任意打乱的标号，若能使得两者相等，则称两者等价。

记为全体置换，定义为等价类的集合。

这作用相当于将中提供的标号抹去。对于上例：其中代表了等价类。

子结构构造（Substitution 构造）

现有组合类，其中是“标号无关的”，记为全体置换，定义“子结构构造”为：

考虑计数。首先观察中等价类的大小，由于是“标号无关的”，对施加种标号交换得到的元素都仍在中，它们能产生对应的。由于分配到了不同的标号，它们互不相同，所以所有打乱产生的复合对象都互不相同，故等价类大小总是，除去即可。

对于，记，则

在有标号计数中，诸多组合构造都能由 Subsitution 构造导出。

构造

大小为的有标号序列有个。记为有标号序列，为序列的 EGF，有若，则
构造

大小为的有标号环有个。记为有标号环，为环的 EGF，有若，则
构造

大小为的有标号无序集合只有个。记为有标号无序集合，为其 EGF，有若，则

相比面相置换群的推导，它们更简单直接。

Erase/Rewrite 构造

操作末标号

对于有标号组合对象，定义：
- 擦去最大的标号，对应元素变为无标号元素。
- 写回最大的标号。

例：对于，可以理解为将最大标号藏起来，不参与分配，最后再将其恢复。即最大标号一定分配给了中对象。

具体地（用表示擦去）：比较和，能看出，在后者中，标号一定分配给中对象。

注意，不能对双方都进行再，这样后者分不清最大值应该给哪边，是不良定义的。

相当于将组合对象的大小减少一，则是让大小增加一（此处的大小就是标号个数）。写成生成函数的形式，恰是系数的平移

当然，和也可以视作擦除/重写最小标号。它们的具体组合意义可以依语境而定。

有根组合对象

若组合对象有且仅有一个元素是特殊的（可以认为有一个无大小的标记），称作根，则该组合对象为“有根对象”，对应的组合类为“有根组合类”。

称根元素的标号为“根标号”。
操作根标号

对于标号无关的有根组合对象，定义组合变换：
- 删除根的标号，根元素变成无标号元素，其余元素标号离散化。
- 恢复根的标号。

例如，记为某些有根有序有标号二叉树（方形节点代表根）：

有

接下来考虑计算。对于有根组合类，记为大小为的集合（此处定义为含个标号，而非含个节点，因为二项卷积由标号决定），删除根的标号后，大小会变为，且根原来的标号方案有种（因为标号无关，种方法一定都成立）。

由此，记，则

写成生成函数的形式，恰好是乘除：

例：非空有标号有根树删除根，就变成一个无标号根下的有标号森林，与有标号森林一一对应。记“非空有标号有根”为，“可空有标号森林”为，则